Exam 12: What Is Algebra
Exam 1: Reasoning About Quantities34 Questions
Exam 2: Numeration Systems96 Questions
Exam 3: Understanding Whole Number Operations66 Questions
Exam 4: Some Conventional Ways of Computing17 Questions
Exam 5: Using Numbers in Sensible Ways38 Questions
Exam 6: Meanings for Fractions85 Questions
Exam 7: Computing With Fractions54 Questions
Exam 8: Multiplicative Comparisons and Multiplicative Reasoning19 Questions
Exam 9: Ratios, Rates, Proportions, and Percents33 Questions
Exam 10: Integers and Other Number Systems24 Questions
Exam 11: Number Theory57 Questions
Exam 12: What Is Algebra28 Questions
Exam 13: A Quantitative Approach to Algebra and Graphing18 Questions
Exam 14: Understanding Change: Relationships Among Time, Distance, and Rate10 Questions
Exam 15: Further Topics in Algebra and Change55 Questions
Exam 16: Polygons75 Questions
Exam 17: Polyhedra51 Questions
Exam 18: Symmetry17 Questions
Exam 19: Tessellations9 Questions
Exam 20: Similarity47 Questions
Exam 21: Curves, Constructions, and Curved Surfaces17 Questions
Exam 22: Transformation Geometry24 Questions
Exam 23: Measurement Basics21 Questions
Exam 24: Area, Surface Area, and Volume27 Questions
Exam 25: Counting Units Fast: Measurement Formulas31 Questions
Exam 26: Special Topics in Measurement21 Questions
Exam 27: Quantifying Uncertainty39 Questions
Exam 28: Determining More Complicated Probabilities37 Questions
Exam 29: Introduction to Statistics and Sampling7 Questions
Exam 30: Representing and Interpreting Data With One Variable32 Questions
Exam 31: Dealing With Multiple Data Sets or With Multiple Variables8 Questions
Exam 32: Variability in Samples21 Questions
Exam 33: Special Topics in Probability16 Questions
Select questions type
Use specific values for m and n in
to give a basis for justifying that
.
Free
(Essay)
4.9/5  (30)
(30)
Correct Answer:
Let Then So , when squared, gives a. That is, must be
.
Test each algebra statement to see whether they appear to be true in general. If a statement appears always to be true, draw a diagram to justify the statement. Add an explanation if the diagram is not self-explanatory. If a statement is not true in general, give a counterexample.
A)
B)
C)
D)
E)
Free
(Essay)
4.9/5  (33)
(33)
Correct Answer:
A) Not true in general; student should have shown a counterexample.
B) True. Sample diagram: 
C) Not true in general; student should have shown a counterexample.
D) Not true in general; student should have shown a counterexample.
E) Not true in general; student should have shown a counterexample.
Complete the following and tell how they are alike.
A)
B)
Free
(Essay)
4.8/5  (32)
(32)
Correct Answer:
A)
B)
The two are alike in finding a common denominator and in simplifying toward the end.
Over a four-day period, one Girl Scout troop sold 178 boxes of cookies on the first day, 39 more boxes on the third day than on the second day, and 10 boxes fewer on the fourth day than on the second day. The troop sold 489 boxes in the four days. How many boxes did they sell each day?
(Essay)
4.8/5  (32)
(32)
Does each of the following give a function? Include correct reasons for credit.
A) Associate with each whole number n its third power n 3.
B) Assign to each person in the town his/her current last name.
C) Assign to the last names of people in town the first names.
D) The ordered pairs (5, 2), (7, 2), and (4, 9)
E) This dot diagram:
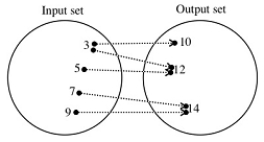
(Essay)
4.9/5  (42)
(42)
The "balance" diagram below shows x + 2 = x3. (If it is not true, give a correct equation.) 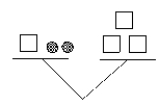
(True/False)
4.9/5  (39)
(39)
Express symbolically, using variables, the general properties in algebra that are illustrated.
A)
B)
C)
D)
(Essay)
4.9/5  (41)
(41)
Take-home question: Here are examples of a shortcut for mentally squaring a number.
Example 1) 762: Go to the closest multiple of 10-here, for 76, plus 4 to 80. Then go the opposite way from 76 by the same amount, minus 4 to 72. Multiply 80 and 72 mentally for 5760. Add the square of the up-down number 4. As a result, 5760 + 16 = 5776 and 762 = 5776.
Example 2) 622: Go to 60 (down 2). Then go up from 62 by 2 to 64. Therefore, 60 × 64 = 3840. Add the square of 2 for 622 = 3844.
Example 3) 572: Go to 60 then 54. Therefore, 60 × 54 = 3240. Add 32 for 572 = 3249.
Example 4) 1982: 200 × 196 = 39,200. Add 22 for 39,204 (= 1982).
A) Use the shortcut to calculate 372 mentally, and then write the mental steps you did.
B) Give a justification that the method works for squaring any n. Label the up-down number x.
(Essay)
4.9/5  (25)
(25)
The repeating decimal for is 3.2715427154…. What digit is in the 99th decimal place in the repeating decimal? Explain how you know.
(Essay)
4.9/5  (31)
(31)
Finish each story problem so that it can be described by the given equation.
A) 50 - n = 16: "Jamal had 50 pieces of paper …"
B) 3n + 16.99 = 37: "Jose went shopping and bought a CD for $16.99 …"
(Essay)
4.7/5  (32)
(32)
A child is making "space modules with antennas" from toothpicks. 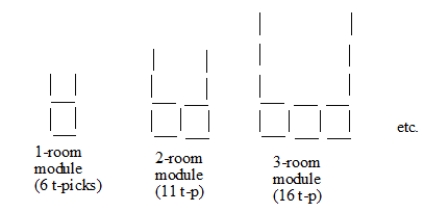 The child wonders, "How many toothpicks would it take to make a 100-room module with antennas?!"
The child wonders, "How many toothpicks would it take to make a 100-room module with antennas?!"
(Essay)
4.7/5  (30)
(30)
A) Part I: It is correct that 12nine × 32nine = 384nine. How might that inform ?
B) Part II: Explain the "might" in part A by considering 4nine × 13nine = 53nine. Give another calculation that would misinform an algebraic expression. Bonus: Why does 4nine × 13nine = 53nine, or your calculation, give an incorrect idea for algebra?
(Essay)
4.8/5  (36)
(36)
You find a function rule for a given table of data. Explain why your answer might not be the correct one.
(Essay)
4.7/5  (35)
(35)
Name the property (or properties) that justifies each of the following.
A) (700 + 60 + 3) + (200 + 30 + 5) = (3 + 5) + (60 + 30) + (700 + 200)
B) 5 × (17 + 3) = (5 × 17) + (5 × 3)
C) 984 + (717 + 563) = 984 + (563 + 717)
D) (56 × 89) ×
= 56 × 89
E)
(Hint: More than one property!)
F)
G)
H) 5 × (17 × 3) = 5 × (3 × 17)
(Essay)
4.8/5  (29)
(29)
In each part, use the given, correct algebraic statements to answer the calculations.
A) Part I:
implies that 14seventeen × 21seventeen = _____seventeen.
B) Part II:
implies that 23eleven × 21eleven = _____eleven.
C) Bonus: What other bases could be used in parts I and II?
(Essay)
4.8/5  (41)
(41)
Give the 100th and the nth entries for these lists, assuming the patterns continue. A) 100th nth
B) 100th nth
C) 100th nth
(Short Answer)
4.8/5  (34)
(34)
Show your mastery of the conventional order of operations by evaluating each.
A) 6 + 3 × 7 - (2 + -1) 5
B) 10 - 4 ÷ 3 × 2 + 1
C) 10 - 4 ÷ 3 × (2 + 1)
D) , when
E) , when
(Short Answer)
4.8/5  (38)
(38)
Suppose g(x) = 3x - 2, and h(x) is defined by machine X below. What number is each of the following? Show your work. 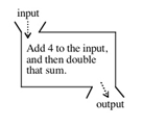 A) g(10) + g(5)
B) h(20)
A) g(10) + g(5)
B) h(20)
(Short Answer)
4.7/5  (34)
(34)
Showing 1 - 20 of 28
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)