Exam 3: Understanding Whole Number Operations
Exam 1: Reasoning About Quantities34 Questions
Exam 2: Numeration Systems96 Questions
Exam 3: Understanding Whole Number Operations66 Questions
Exam 4: Some Conventional Ways of Computing17 Questions
Exam 5: Using Numbers in Sensible Ways38 Questions
Exam 6: Meanings for Fractions85 Questions
Exam 7: Computing With Fractions54 Questions
Exam 8: Multiplicative Comparisons and Multiplicative Reasoning19 Questions
Exam 9: Ratios, Rates, Proportions, and Percents33 Questions
Exam 10: Integers and Other Number Systems24 Questions
Exam 11: Number Theory57 Questions
Exam 12: What Is Algebra28 Questions
Exam 13: A Quantitative Approach to Algebra and Graphing18 Questions
Exam 14: Understanding Change: Relationships Among Time, Distance, and Rate10 Questions
Exam 15: Further Topics in Algebra and Change55 Questions
Exam 16: Polygons75 Questions
Exam 17: Polyhedra51 Questions
Exam 18: Symmetry17 Questions
Exam 19: Tessellations9 Questions
Exam 20: Similarity47 Questions
Exam 21: Curves, Constructions, and Curved Surfaces17 Questions
Exam 22: Transformation Geometry24 Questions
Exam 23: Measurement Basics21 Questions
Exam 24: Area, Surface Area, and Volume27 Questions
Exam 25: Counting Units Fast: Measurement Formulas31 Questions
Exam 26: Special Topics in Measurement21 Questions
Exam 27: Quantifying Uncertainty39 Questions
Exam 28: Determining More Complicated Probabilities37 Questions
Exam 29: Introduction to Statistics and Sampling7 Questions
Exam 30: Representing and Interpreting Data With One Variable32 Questions
Exam 31: Dealing With Multiple Data Sets or With Multiple Variables8 Questions
Exam 32: Variability in Samples21 Questions
Exam 33: Special Topics in Probability16 Questions
Select questions type
A visitor to a first-grade classroom sees a teacher ask a student to solve this problem:
Jaime gets $5 a week for keeping the yard in good shape. He is saving his money for the county fair. After four weeks, how much has he saved?
A) The visitor thinks to himself, "This is a multiplication problem, and first-graders have not yet been taught multiplication, so they can't answer this problem." But after a few minutes, the first-grader says that the answer is 20. The student explains how she did this problem, and, much to the visitor's surprise, she did not do any formal multiplication. What did she most likely do to find the answer?
B) This visitor also sees the students work another problem: 8 miles of highway are being paved. If the workers pave 2 miles a day, how long will it take them to pave all 8 miles? The visitor thinks, "This is a division problem and first-graders have not yet learned to divide." But then one student says that it would take four days. How do you suppose she explained this answer without using division?
Free
(Short Answer)
4.8/5  (25)
(25)
Correct Answer:
A) She probably used repeated addition: 5 and 5 is 10, and 5 more is 15, and 5 more is 20.
B) She probably subtracted 2 from 8 four times, until she reached 0, and then counted the number of times she subtracted 2--four times.
To determine how much older than you your father is, you need to make an additive comparison of his and your ages.
Free
(True/False)
4.9/5  (43)
(43)
Correct Answer:
True
I am a number with 21 tens, 14 ones, and 11 tenths. What number am I?
Free
(Short Answer)
4.9/5  (36)
(36)
Correct Answer:
225.1
Make up a story problem about a bake sale so that the problem could be solved by:
A) 3/4 × 12. (Notice the order.)
B) 12 × 3/4 .
(Essay)
4.9/5  (37)
(37)
Tell why the following calculations are INCORRECT.
A)
Sum: 310 225 980 1895
B) 280 ÷ 70 = 40
C) 480 ÷ 0.4 = 120
(Essay)
4.8/5  (46)
(46)
The product of a number n by any other number m different from 0 is always greater than n.
(True/False)
4.9/5  (27)
(27)
Is this child's thinking correct? If it is, complete the second calculation using the child's method. If the thinking is not correct, explain why not. (given) (child does) 675 677 -198 -200 477
Second calculation (or explanation if not correct):
453 -295
(Short Answer)
4.8/5  (44)
(44)
Amy finds 32 × 54 as follows:
54 is 4 more than 50, so find 32 × 50 and add 4 back to get 1728.
A) Which is TRUE of Amy's mathematical steps?
i. Amy's steps are probably mathematically correct, although the phrasing is not perfect (should be "add four 32s back").
ii. Amy's steps are mathematically flawed.
iii. It cannot be determined whether Amy's steps are mathematically correct or flawed.
B) Which is TRUE of Amy's understanding of multiplication?
i. Amy doesn't appear to understand multiplication.
ii. Amy may or may not understand multiplication.
iii. Amy shows good understanding of multiplication.
(Essay)
4.8/5  (45)
(45)
Of the expressions 0 ÷ 6, 6 ÷ 0, and 0 ÷ 0, which is/are undefined? Explain why any undefined choice(s) is/are undefined. If the expression is defined, tell what it equals.
(Essay)
4.9/5  (37)
(37)
A student wrote the following answer to the problem 95 - 34:
95 - 34 =
95 - 35 = 60
60 - 1 = 59
So the answer is 59
Analyze this student's thinking.
(Essay)
4.8/5  (30)
(30)
A bill for school supplies was $87.35. Josh paid with two $50 bills. Rikki, at the cash register (one that did not tell the change to be given to the buyer), counted Josh's change: "40, 50, $1, and $10 makes $100." How much change did Josh receive? In what currency? Is that what he should have received?
(Essay)
4.7/5  (21)
(21)
Following is only the start of a child's work (in base ten). What seems lacking in this child's understanding? (Assume, perhaps unfairly, that the child is not thinking of negative numbers.) 402 \ldots7 506 \ldots3
(Essay)
4.7/5  (36)
(36)
In each scenario, which way of thinking about subtraction is involved?
A) Story problem: Basketball score: Aztecs 82, Opponents 69. By how many points did the Aztecs win?
B) Thinking/drawing strategy (sometimes used with children having trouble with their basic subtraction facts): For 15 - 7, think of going "up the hill," going to 10 along the way…
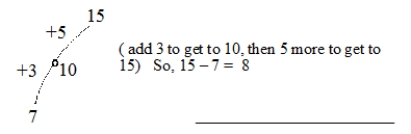
(Short Answer)
4.9/5  (42)
(42)
Following is an example of a child's work. Study the work and then judge the student's understanding.
Hiro was asked to divide 4240 by 6. His work is shown below.
Hiro's work: 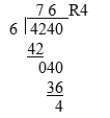 A) Is Hiro's work correct or incorrect?
B) If the work is incorrect, please explain how.
A) Is Hiro's work correct or incorrect?
B) If the work is incorrect, please explain how.
(Short Answer)
4.8/5  (33)
(33)
In which word problem (A or B) is there an action involved that may make it easier for young children to solve?
(Multiple Choice)
4.9/5  (31)
(31)
Mitchell decides to get his car painted and to buy new hubcaps. He selects five colors he likes and three styles of hubcaps. Then he decides to paint the roof a different color than the body. He decides to let his wife make the final decision. How many choices does she have?
(Short Answer)
4.9/5  (34)
(34)
Showing 1 - 20 of 66
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)