Exam 28: Determining More Complicated Probabilities
Exam 1: Reasoning About Quantities34 Questions
Exam 2: Numeration Systems96 Questions
Exam 3: Understanding Whole Number Operations66 Questions
Exam 4: Some Conventional Ways of Computing17 Questions
Exam 5: Using Numbers in Sensible Ways38 Questions
Exam 6: Meanings for Fractions85 Questions
Exam 7: Computing With Fractions54 Questions
Exam 8: Multiplicative Comparisons and Multiplicative Reasoning19 Questions
Exam 9: Ratios, Rates, Proportions, and Percents33 Questions
Exam 10: Integers and Other Number Systems24 Questions
Exam 11: Number Theory57 Questions
Exam 12: What Is Algebra28 Questions
Exam 13: A Quantitative Approach to Algebra and Graphing18 Questions
Exam 14: Understanding Change: Relationships Among Time, Distance, and Rate10 Questions
Exam 15: Further Topics in Algebra and Change55 Questions
Exam 16: Polygons75 Questions
Exam 17: Polyhedra51 Questions
Exam 18: Symmetry17 Questions
Exam 19: Tessellations9 Questions
Exam 20: Similarity47 Questions
Exam 21: Curves, Constructions, and Curved Surfaces17 Questions
Exam 22: Transformation Geometry24 Questions
Exam 23: Measurement Basics21 Questions
Exam 24: Area, Surface Area, and Volume27 Questions
Exam 25: Counting Units Fast: Measurement Formulas31 Questions
Exam 26: Special Topics in Measurement21 Questions
Exam 27: Quantifying Uncertainty39 Questions
Exam 28: Determining More Complicated Probabilities37 Questions
Exam 29: Introduction to Statistics and Sampling7 Questions
Exam 30: Representing and Interpreting Data With One Variable32 Questions
Exam 31: Dealing With Multiple Data Sets or With Multiple Variables8 Questions
Exam 32: Variability in Samples21 Questions
Exam 33: Special Topics in Probability16 Questions
Select questions type
Experiment: Spin Spinner 1 (below) and note the number. Then spin Spinner 2 and note the number.
A) Make a tree diagram for this experiment, with probabilities on the branches of the tree.
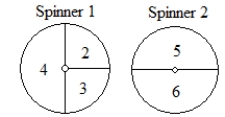 B) Give the sample space for the experiment and the associated probabilities.
C) P(the first spin is an even number) = ______
D) P(the sum of the two spins = 9) = ______
E) P(the first spin is an even number or the sum of the two spins = 9) = ______
B) Give the sample space for the experiment and the associated probabilities.
C) P(the first spin is an even number) = ______
D) P(the sum of the two spins = 9) = ______
E) P(the first spin is an even number or the sum of the two spins = 9) = ______
Free
(Essay)
4.8/5  (32)
(32)
Correct Answer:
A.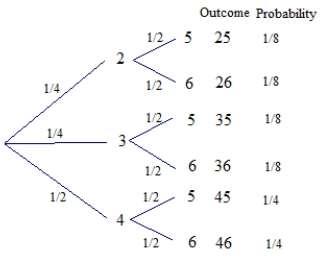
B) See the answer for part A.
C) 3/4
D) 1/8 + 1/4 = 3/8
E) 3/4 + 3/8 - 1/4 = 7/8
A future birth order of BGBG has the same probability as does GGGG.
Free
(True/False)
4.7/5  (31)
(31)
Correct Answer:
True
Below is a probability tree diagram for an experiment. If the probability of BD is 0.48, what is the probability of AC?
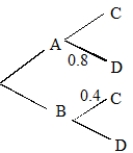
Free
(Essay)
4.8/5  (32)
(32)
Correct Answer:
0.2 × 0.2 = 0.04 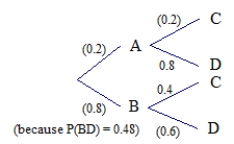
If A and B are not disjoint events, then P(A or B) < P(A) + P(B).
(True/False)
4.8/5  (33)
(33)
If events A and B are independent with P(A) = 0.4 and P(B) = 0.2, then P(A and B) = 0.8.
(True/False)
4.8/5  (25)
(25)
If you buy a blouse at random from the Sands End catalog, P(blue blouse) = 0.3 and P(frilly sleeves) = 0.2.
A) Find P(blue blouse or frilly sleeves). Show your work for credit.
B) What assumption did you make in part A? Justify your assumption for this situation.
(Essay)
4.8/5  (34)
(34)
In tossing eight honest coins, HTHHTHTT is more probable than TTTTTTTT.
(True/False)
4.9/5  (34)
(34)
Suppose that in your work you often deal with complicated events, as in the drawing below. (The circular regions show events.) Write a formula for how you could calculate P(A or B or C), using simpler probabilities like P(A) and so on. 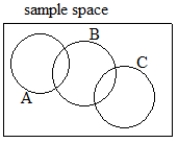
(Essay)
4.8/5  (33)
(33)
Experiment: Spin the spinner below and note the number. Then spin the spinner again and note the number. 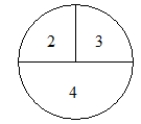 A) Give the sample space for the whole experiment.
B) P(first spin gives 3) = ______
C) What does your answer in part B mean? (If you can't answer part B, use a fake answer for it to answer part c.)
D) P(the sum of the two numbers = 6) = ______
A) Give the sample space for the whole experiment.
B) P(first spin gives 3) = ______
C) What does your answer in part B mean? (If you can't answer part B, use a fake answer for it to answer part c.)
D) P(the sum of the two numbers = 6) = ______
(Essay)
4.9/5  (41)
(41)
A company has collected data on the numbers of male and female employees who did or did not graduate from college. The data are summarized below. (Hint: Make a table before answering the questions.)
If an employee is selected from this company, find the following probabilities. College Graduate College Graduate College Graduate Yes No Male 198 9 Female 190 3
If an employee is selected from this company, find the following probabilities.
A) P(female and college graduate)
B) P(female or college graduate)
C) P(female | college graduate)
D) P(college graduate | female)
(Essay)
4.7/5  (34)
(34)
Karen asked her dad for two dimes to buy gumballs for herself and her brother. (The machine gives one gumball for a dime.) There were three red gumballs, two yellow gumballs, and one green gumball in the machine. Her favorite gumball is red. She hopes that she will get at least one red gumball.
A) List all the possible outcomes she can get for the two gumballs (think carefully) and the probabilities for each.
B) What is the probability that Karen will get at least one red gumball?
C) What does your answer in part B mean?
(Essay)
4.9/5  (37)
(37)
Suppose that in your work you often deal with complicated events as in the drawing below. Write a formula for how you could calculate P(A or B or C), using simpler probabilities like P(A) and so on. 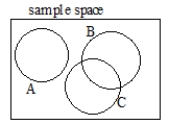
(Essay)
4.9/5  (30)
(30)
Give a formula for P(A or B or C) for events like those shown below, using simpler probabilities like P(A) and so on. 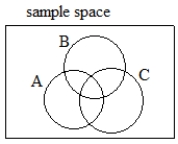
(Essay)
4.7/5  (41)
(41)
For events A and B, if P(A) = 0.2 and P(B) = 0.4, then P(A or B) = 0.6.
(True/False)
5.0/5  (36)
(36)
Experiment: Spin Spinner 1 (below) and note the number. Then spin Spinner 2 and note the number.
A) Make a tree diagram for this experiment, with all the final outcomes and the probabilities for each outcome.
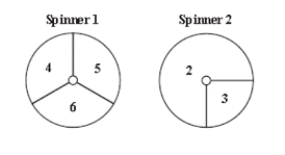 B) P(the first spin is an even number) = ______
C) P(the sum of the two spins = 7) = ______
D) P(the first spin is an even number or the sum of the two spins = 7) = ______
B) P(the first spin is an even number) = ______
C) P(the sum of the two spins = 7) = ______
D) P(the first spin is an even number or the sum of the two spins = 7) = ______
(Essay)
4.8/5  (43)
(43)
The probability of guessing correctly on all of five true-false questions is
(True/False)
4.8/5  (31)
(31)
A school tried out two curricula, P and Q, with a total of 200 children. Average or above average Below average Curriculum P Curriculum Q 200
A) 60% of the 200 children studied curriculum P. Enter that number of children in the appropriate place in the contingency table.
B) 30% of all the children scored below average on the state test. Enter that number of children in the appropriate place in the table.
C) of the curriculum Q children scored below average. Enter that number of children in the appropriate place in the table.
D) Given that a child studied curriculum P, what is the probability that the child scored average or above average on the state test?
E) Given that child studied curriculum Q, what is the probability that the child scored average or above average on the state test?
(Essay)
4.7/5  (31)
(31)
Experiment: Draw a ball from Box 1, note its color, and then put the ball into Box 2. Then draw a ball from Box 2 and note its color.
A) Make a condensed tree diagram for this experiment, with probabilities on the branches.
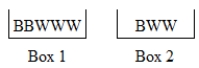 B) Write the probabilities for each outcome of the experiment. (Write them on the tree diagram in part
C) For this experiment, what is the probability of the event "the second ball is B"?
B) Write the probabilities for each outcome of the experiment. (Write them on the tree diagram in part
C) For this experiment, what is the probability of the event "the second ball is B"?
(Essay)
4.9/5  (30)
(30)
A) Make a condensed tree diagram for this experiment. Spin and then select one ball from the box designated by the spinner. Record the outcomes and their probabilities. 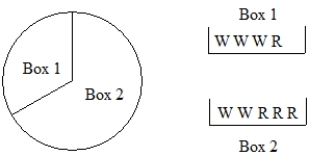 B) What is the probability of drawing an R?
B) What is the probability of drawing an R?
(Essay)
4.8/5  (25)
(25)
A box has 3 green balls (G) and 2 red balls (R). Experiment: Draw a ball and note its color. Do not put it back. Draw again and note the color.
A) Make a condensed tree diagram for the experiment, complete with probabilities for the outcomes.
B) What is the probability that the two balls drawn are the same color?
(Essay)
4.9/5  (34)
(34)
Showing 1 - 20 of 37
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)