Exam 5: Finitely-Repeated, Static Games
Exam 1: Introduction to Game Theory35 Questions
Exam 2: Noncooperative, One-Time, Static Games86 Questions
Exam 3: Focal-Point and Evolutionary Equilibria32 Questions
Exam 4: Infinitely-Repeated, Static Games37 Questions
Exam 5: Finitely-Repeated, Static Games40 Questions
Exam 6: Mixing Pure Strategies51 Questions
Exam 7: Static Games With Continuous Strategies24 Questions
Exam 8: Imperfect Competition52 Questions
Exam 9: Perfect Competition and Monopoly33 Questions
Exam 10: Strategic Trade Policy35 Questions
Exam 11: Dynamic Games With Complete47 Questions
Exam 12: Bargaining54 Questions
Exam 13: Pure Strategies With Uncertain Payoffs65 Questions
Exam 14: Torts and Contracts45 Questions
Exam 15: Auctions44 Questions
Exam 16: Dynamic Games With Incomplete Information34 Questions
Select questions type
 -Consider the oil-drilling game depicted in Figure 5.4 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will end in the next round is 10 percent and the discount rate is 25 percent. What is the present value of the stream of payoffs by cooperating?
-Consider the oil-drilling game depicted in Figure 5.4 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will end in the next round is 10 percent and the discount rate is 25 percent. What is the present value of the stream of payoffs by cooperating?
(Multiple Choice)
4.9/5  (28)
(28)
 -Consider the pricing game depicted in Figure 5.5 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will end in the next stage is 5 percent. For what discount rate will a firm be indifferent between cooperating and defecting?
-Consider the pricing game depicted in Figure 5.5 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will end in the next stage is 5 percent. For what discount rate will a firm be indifferent between cooperating and defecting?
(Multiple Choice)
5.0/5  (32)
(32)
 -Consider the noncooperative oil-drilling game depicted in Figure 5.4 in which payoffs are in millions of dollars. If this game is played five times, the Nash equilibrium strategy profile in the first round is:
-Consider the noncooperative oil-drilling game depicted in Figure 5.4 in which payoffs are in millions of dollars. If this game is played five times, the Nash equilibrium strategy profile in the first round is:
(Multiple Choice)
4.9/5  (28)
(28)
 -Consider the pricing game depicted in Figure 5.5 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will end in the next stage is 1 percent. For what discount rate will a firm be indifferent between cooperating and defecting?
-Consider the pricing game depicted in Figure 5.5 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will end in the next stage is 1 percent. For what discount rate will a firm be indifferent between cooperating and defecting?
(Multiple Choice)
4.7/5  (39)
(39)
 -Consider the pricing game depicted in Figure 5.5 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the discount rate is 1 percent. What is the probability that the game will end if the players are indifferent between cooperating and defecting?
-Consider the pricing game depicted in Figure 5.5 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the discount rate is 1 percent. What is the probability that the game will end if the players are indifferent between cooperating and defecting?
(Multiple Choice)
4.8/5  (25)
(25)
 -Consider the pricing game depicted in Figure 5.5 in which the payoffs are in millions of dollars. If this game is played seven times, the Nash equilibrium strategy profile in the first stage is:
-Consider the pricing game depicted in Figure 5.5 in which the payoffs are in millions of dollars. If this game is played seven times, the Nash equilibrium strategy profile in the first stage is:
(Multiple Choice)
4.8/5  (40)
(40)
 -Consider the pricing game depicted in Figure 5.5 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the discount rate is 5 percent. What is the probability that the game will end if the players are indifferent between cooperating and defecting?
-Consider the pricing game depicted in Figure 5.5 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the discount rate is 5 percent. What is the probability that the game will end if the players are indifferent between cooperating and defecting?
(Multiple Choice)
4.9/5  (37)
(37)
The probability that a two-player, repeated game comes to an end in each stage is 2. When 2 = 1, this game may be treated as:
(Multiple Choice)
4.9/5  (29)
(29)
The probability that a two-player, repeated game comes to an end in each stage is 2. When 0 < 2 < 1, this game may be treated as:
(Multiple Choice)
4.7/5  (34)
(34)
_____ is when a finitely-repeated game a certain end reduces to a series of one-time, static games.
(Multiple Choice)
4.8/5  (28)
(28)
 -Consider the two-stage, static game depicted in Figure 5.1 involving two companies that enter into an agreement to maximize total profits. The payoffs in this game are in millions of dollars. The optimal strategy for both firms is to:
-Consider the two-stage, static game depicted in Figure 5.1 involving two companies that enter into an agreement to maximize total profits. The payoffs in this game are in millions of dollars. The optimal strategy for both firms is to:
(Multiple Choice)
4.7/5  (40)
(40)
In the text, the publishing company Houghton Mifflin was able to thwart Western Pacific's takeover bid by threatening to release its best-selling authors from their contractual obligations. This is an example of:
(Multiple Choice)
4.8/5  (35)
(35)
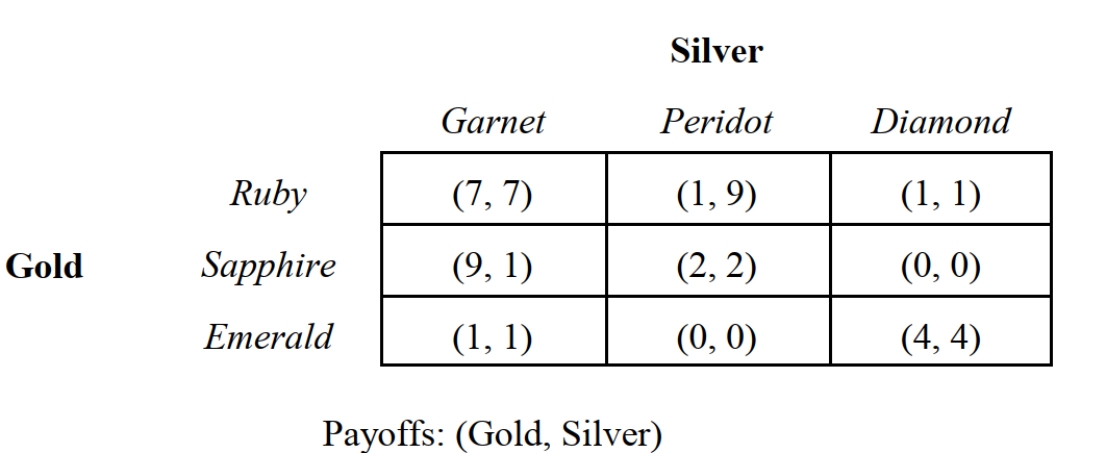 -Consider the two-stage game depicted in Figure 5.3 involving two companies that enter into an agreement to maximize total profits. The payoffs in this game are in millions of dollars. Silver's optimal strategy is to:
-Consider the two-stage game depicted in Figure 5.3 involving two companies that enter into an agreement to maximize total profits. The payoffs in this game are in millions of dollars. Silver's optimal strategy is to:
(Multiple Choice)
4.8/5  (24)
(24)
Showing 21 - 40 of 40
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)