Exam 4: Applications of the Derivative
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Which of the graphs shows the solution of the given initial value problem?
-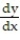 = -2x, y = -2 when x = -1
= -2x, y = -2 when x = -1
(Multiple Choice)
4.8/5  (36)
(36)
Find the extreme values of the function and where they occur.
-y = 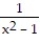
(Multiple Choice)
4.9/5  (27)
(27)
Solve the problem.
-On our moon, the acceleration of gravity is 1.6 m/ 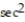 . If a rock is dropped into a crevasse, how fast will it be going just before it hits bottom 45 seconds later?
. If a rock is dropped into a crevasse, how fast will it be going just before it hits bottom 45 seconds later?
(Multiple Choice)
4.9/5  (39)
(39)
Choose the one alternative that best completes the statement or answers the question.
-The positions of two particles on the s-axis are 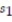 = sin t and
= sin t and 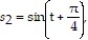 with
with  and
and  in meters and t in seconds. At what time(s) in the interval 0 t 2 do the particles meet?
in meters and t in seconds. At what time(s) in the interval 0 t 2 do the particles meet?
(Multiple Choice)
4.8/5  (35)
(35)
Find the value or values of c that satisfy the equation ![Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = ln (x - 3), [ 4, 8]](https://storage.examlex.com/TB9662/11ee9522_3416_08b0_bdb6_3b3290666101_TB9662_11.jpg) =
= ![Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = ln (x - 3), [ 4, 8]](https://storage.examlex.com/TB9662/11ee9522_3416_08b1_bdb6_a738a1f77c49_TB9662_11.jpg) (c) in the conclusion of the Mean Value Theorem for the function and interval.
-f(x) = ln (x - 3), [ 4, 8]
(c) in the conclusion of the Mean Value Theorem for the function and interval.
-f(x) = ln (x - 3), [ 4, 8]
(Multiple Choice)
4.9/5  (34)
(34)
Choose the one alternative that best completes the statement or answers the question.
-The 9 ft wall shown here stands 30 feet from the building. Find the length of the shortest straight beam that will reach to the side of the building from the ground outside the wall.
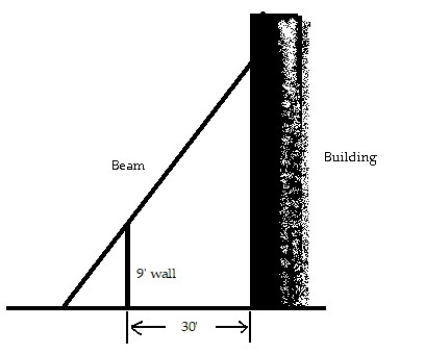
(Multiple Choice)
4.8/5  (40)
(40)
Determine all critical points for the function.
-f(x) = 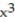 - 9
- 9 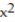 + 10
+ 10
(Multiple Choice)
5.0/5  (32)
(32)
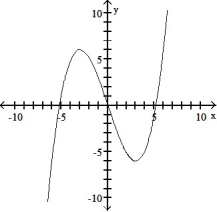
Use the graph of the function f(x) to locate the local extrema and identify the intervals where the function is concave up and concave down.
-
(Multiple Choice)
4.9/5  (38)
(38)
Solve the initial value problem.
-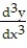 = 9;
= 9; 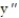 (0) = -5,
(0) = -5, 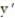 (0) = 6, y(0) = 5
(0) = 6, y(0) = 5
(Multiple Choice)
4.9/5  (32)
(32)
Find the linearization L(x) of f(x) at x = a.
-f(x) = 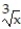 , a = 8
, a = 8
(Multiple Choice)
4.8/5  (38)
(38)
Use a calculator to compute the first 10 iterations of Newton's method when applied to the function with the given initial approximation. Make a table for the values. Round to six decimal places.
-f(x) = 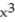 + x - 9;
+ x - 9; 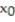 = 1
= 1
(Multiple Choice)
4.7/5  (41)
(41)
Express the relationship between a small change in x and the corresponding change in y in the form 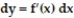 .
-y = 5
.
-y = 5 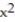 - 2x - 7
- 2x - 7
(Multiple Choice)
4.9/5  (42)
(42)
Use Newton's method to approximate all the intersection points of the pair of curves. Some preliminary graphing or analysis may help in choosing good initial approximations. Round to six decimal places.
-y = ln(x + 5) and y = 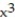
(Multiple Choice)
4.9/5  (39)
(39)
Use differentiation to determine whether the integral formula is correct.
-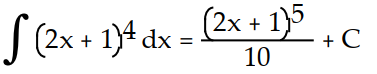
(True/False)
4.7/5  (32)
(32)
Find the extreme values of the function and where they occur.
-y = x3 - 12x + 2
(Multiple Choice)
4.8/5  (38)
(38)
Showing 41 - 60 of 228
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)