Exam 4: Applications of the Derivative
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Use differentiation to determine whether the integral formula is correct.
-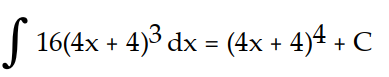
(True/False)
4.8/5  (45)
(45)
Find the value or values of c that satisfy the equation ![Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = + 2x + 1, [ -3, -2]](https://storage.examlex.com/TB9662/11ee9522_3416_08b0_bdb6_3b3290666101_TB9662_11.jpg) =
= ![Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = + 2x + 1, [ -3, -2]](https://storage.examlex.com/TB9662/11ee9522_3416_08b1_bdb6_a738a1f77c49_TB9662_11.jpg) (c) in the conclusion of the Mean Value Theorem for the function and interval.
-f(x) =
(c) in the conclusion of the Mean Value Theorem for the function and interval.
-f(x) = ![Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = + 2x + 1, [ -3, -2]](https://storage.examlex.com/TB9662/11ee9522_3416_08b2_bdb6_532cc9f6e27f_TB9662_11.jpg) + 2x + 1, [ -3, -2]
+ 2x + 1, [ -3, -2]
(Multiple Choice)
4.7/5  (36)
(36)
Solve the problem.
-Given the acceleration, initial velocity, and initial position of a body moving along a coordinate line at time t, find the body's position at time t. a = 20, v(0) = 15, s(0) = -11
(Multiple Choice)
4.9/5  (28)
(28)
Provide an appropriate response.
-The position of an object in free fall near the surface of the plane where the acceleration due to gravity has a constant magnitude of g (length-units)/sec2 is given by the equation:
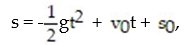 where s is the height above the earth, v0 is the initial velocity, and s0 is the initial height. Give the initial value problem for this situation. Solve it to check its validity. Remember the positive direction is the upward direction.
where s is the height above the earth, v0 is the initial velocity, and s0 is the initial height. Give the initial value problem for this situation. Solve it to check its validity. Remember the positive direction is the upward direction.
(Multiple Choice)
5.0/5  (35)
(35)
Solve the problem.
-The diameter of a tree was 11 in. During the following year, the circumference increased  About how much did the tree's diameter increase? (Leave your answer in terms of .)
About how much did the tree's diameter increase? (Leave your answer in terms of .)
(Multiple Choice)
4.8/5  (35)
(35)
Choose the one alternative that best completes the statement or answers the question.
-A rectangular sheet of perimeter 24 cm and dimensions x cm by y cm is to be rolled into a cylinder as shown in part (a) of the figure. What values of x and y give the largest volume?
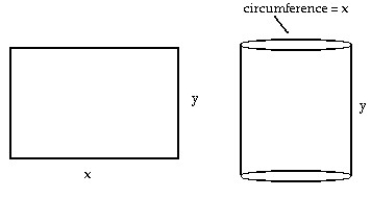
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-Using the following properties of a twice-differentiable function y = f(x), select a possible graph of f.

(Multiple Choice)
4.8/5  (35)
(35)
Choose the one alternative that best completes the statement or answers the question.
-Find the number of units that must be produced and sold in order to yield the maximum profit, given the following equations for revenue and cost: R 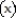 = 6x
C
= 6x
C 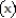 = 0.001
= 0.001 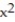 + 1.1x + 60.
+ 1.1x + 60.
(Multiple Choice)
4.9/5  (41)
(41)
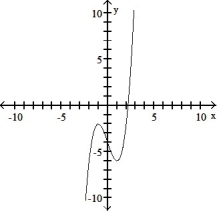
Use the graph of the function f(x) to locate the local extrema and identify the intervals where the function is concave up and concave down.
-
(Multiple Choice)
4.8/5  (42)
(42)
Choose the one alternative that best completes the statement or answers the question.
-Find the number of units that must be produced and sold in order to yield the maximum profit, given the following equations for revenue and cost: R(x) = 60x - 0.5 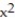 C(x) = 6x + 7.
C(x) = 6x + 7.
(Multiple Choice)
4.7/5  (34)
(34)
Solve the initial value problem.
-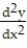 = 4 - 10x,
= 4 - 10x, 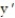 (0) = 8, y(0) = 2
(0) = 8, y(0) = 2
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-An object is dropped from 10 ft above the surface of the moon. How long will it take the object to hit the surface of the moon if 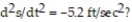
(Multiple Choice)
4.7/5  (33)
(33)
Find the extreme values of the function and where they occur.
-y = x3 - 3x2 + 1
(Multiple Choice)
4.9/5  (28)
(28)
Sketch the graph and show all local extrema and inflection points.
-y = x + sin x, 0 x 2

(Multiple Choice)
4.9/5  (43)
(43)
Showing 101 - 120 of 228
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)