Exam 10: Sequences and Infinite Series
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
A recursion formula and the initial term(s) of a sequence are given. Write out the first five terms of the sequence.
-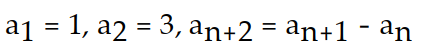
(Multiple Choice)
4.8/5  (34)
(34)
Find a formula for the nth partial sum of the series and use it to find the series' sum if the series converges.
-3 -  +
+ 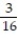 -
- 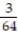 + ... +
+ ... + 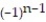
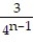 + ...
+ ...
(Multiple Choice)
4.7/5  (43)
(43)
A recursion formula and the initial term(s) of a sequence are given. Write out the first five terms of the sequence.
-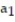 = 1,
= 1, 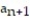 =
= 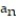 + 5
+ 5
(Multiple Choice)
4.8/5  (46)
(46)
Use the integral test to determine whether the series converges.
-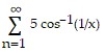
(Multiple Choice)
4.7/5  (37)
(37)
Use the integral test to determine whether the series converges.
-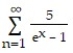
(Multiple Choice)
4.8/5  (44)
(44)
Determine if the series converges or diverges. If the series converges, find its sum.
-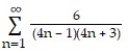
(Multiple Choice)
4.8/5  (37)
(37)
Assume that the sequence converges and find its limit.
-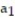 = -2,
= -2, 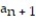 =
= 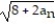
(Multiple Choice)
4.8/5  (37)
(37)
Assume that the sequence converges and find its limit.
-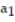 = 5,
= 5, 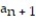 =
= 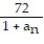
(Multiple Choice)
4.8/5  (34)
(34)
Determine if the series converges or diverges. If the series converges, find its sum.
-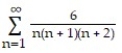
(Multiple Choice)
4.7/5  (28)
(28)
Use the limit comparison test to determine if the series converges or diverges.
-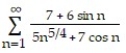
(Multiple Choice)
4.8/5  (47)
(47)
Find the limit of the sequence or determine that the limit does not exist.
-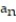 = ln
= ln 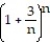
(Multiple Choice)
4.8/5  (38)
(38)
Find a formula for the nth term of the sequence.
-0, 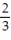 , 0,
, 0, 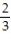 , 0 (alternating 0's and
, 0 (alternating 0's and 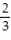 's)
's)
(Multiple Choice)
4.8/5  (37)
(37)
Find a formula for the nth partial sum of the series and use it to find the series' sum if the series converges.
-7 + 63 + 567 + ... + 7 . 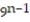 + ...
+ ...
(Multiple Choice)
4.8/5  (39)
(39)
Use the root test to determine if the series converges or diverges.
-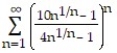
(Multiple Choice)
4.8/5  (34)
(34)
Provide an appropriate response.
-Which of the following is not a condition for applying the integral test to the sequence { 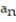 }, where
}, where 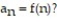 I. f(x) is everywhere positive
II. f(x) is decreasing for x N
III. f(x) is continuous for x N
I. f(x) is everywhere positive
II. f(x) is decreasing for x N
III. f(x) is continuous for x N
(Multiple Choice)
4.8/5  (32)
(32)
Determine if the series converges absolutely, converges, or diverges.
-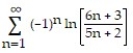
(Multiple Choice)
4.9/5  (41)
(41)
Determine convergence or divergence of the alternating series.
-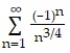
(Multiple Choice)
4.8/5  (36)
(36)
Determine if the series converges absolutely, converges, or diverges.
-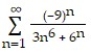
(Multiple Choice)
4.9/5  (34)
(34)
Determine if the series converges absolutely, converges, or diverges.
-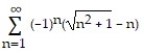
(Multiple Choice)
4.8/5  (34)
(34)
Determine convergence or divergence of the alternating series.
-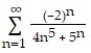
(Multiple Choice)
4.9/5  (34)
(34)
Showing 21 - 40 of 173
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)