Exam 10: Sequences and Infinite Series
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Solve the problem.
-A company's annual revenue for the period since 2000 can be modeled by the function 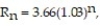 where R is in millions of dollars and n = 0 corresponds to 2000. Assuming the model accurately predicts future revenue, find the year in which the revenue first exceeds $4.98 million.
where R is in millions of dollars and n = 0 corresponds to 2000. Assuming the model accurately predicts future revenue, find the year in which the revenue first exceeds $4.98 million.
(Multiple Choice)
4.9/5  (34)
(34)
Find the limit of the sequence or determine that the limit does not exist.
-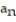 = ln( 9n + 9) - ln( 2n - 7)
= ln( 9n + 9) - ln( 2n - 7)
(Multiple Choice)
4.8/5  (42)
(42)
Find the limit of the sequence if it converges; otherwise indicate divergence.
-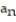 =
= 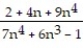
(Multiple Choice)
4.9/5  (38)
(38)
Use the root test to determine if the series converges or diverges.
-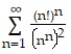
(Multiple Choice)
4.9/5  (36)
(36)
Use the integral test to determine whether the series converges.
-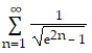
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-A child on a swing sweeps out a distance of 16 ft on the first pass. If she is allowed to continue swinging until she stops, and if on each pass she sweeps out a distance  of the previous pass, how far does the child travel?
of the previous pass, how far does the child travel?
(Multiple Choice)
4.9/5  (36)
(36)
Find a formula for the nth term of the sequence.
-6, 8, 10, 12, 14 (every other integer starting with 6)
(Multiple Choice)
4.8/5  (40)
(40)
Solve the problem.
-A pendulum is released and swings until it stops. If it passes through an arc of 35 inches the first pass, and if on each successive pass it travels 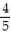 the distance of the preceding pass, how far will it travel before stopping?
the distance of the preceding pass, how far will it travel before stopping?
(Multiple Choice)
5.0/5  (40)
(40)
Use the Comparison Test to determine if the series converges or diverges.
-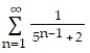
(Multiple Choice)
4.8/5  (45)
(45)
Provide an appropriate response.
-Which of the following sequences do not meet the conditions of the Integral Test?
I. 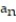 = n(sin n + 1)
II.
= n(sin n + 1)
II. 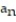 =
= 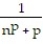 III.
III. 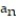 =
= 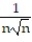
(Multiple Choice)
4.8/5  (42)
(42)
Find a formula for the nth term of the sequence.
--5, -4, -3, -2, -1 (integers beginning with -5)
(Multiple Choice)
4.9/5  (39)
(39)
Use the integral test to determine whether the series converges.
-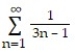
(Multiple Choice)
4.9/5  (52)
(52)
Find a formula for the nth partial sum of the series and use it to find the series' sum if the series converges.
-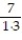 +
+ 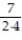 +
+ 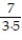 + ... +
+ ... + 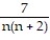 + ...
+ ...
(Multiple Choice)
4.8/5  (40)
(40)
Find the limit of the sequence or determine that the limit does not exist.
-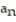 =
= 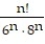
(Multiple Choice)
4.9/5  (38)
(38)
Determine if the geometric series converges or diverges. If it converges, find its sum.
-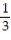 +
+ 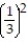 +
+ 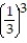 +
+ 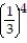 +
+ 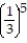 + . . .
+ . . .
(Multiple Choice)
4.8/5  (39)
(39)
Use the Comparison Test to determine if the series converges or diverges.
-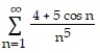
(Multiple Choice)
4.9/5  (31)
(31)
Showing 141 - 160 of 173
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)