Exam 4: Exponential Functions
Exam 1: Linear Functions and Change148 Questions
Exam 2: Functions138 Questions
Exam 3: Quadratic Functions46 Questions
Exam 4: Exponential Functions94 Questions
Exam 5: Logarithmic Functions87 Questions
Exam 6: Transformations of Functions and Their Graphs85 Questions
Exam 7: Trigonometry and Periodic Functions178 Questions
Exam 8: Triangle Trigonometry and Polar Coordinates43 Questions
Exam 9: Trigonometric Identities, Models, and Complex Numbers106 Questions
Exam 10: Compositions, Inverses, and Combinations of Functions69 Questions
Exam 11: Polynomial and Rational Functions145 Questions
Exam 12: Vectors and Matrices104 Questions
Exam 13: Sequences and Series81 Questions
Exam 14: Parametric Equations and Conic Sections128 Questions
Select questions type
The table below shows , the dollar value of a share of a certain stock, as a function of , the time (in weeks) since the initial offering of the stock. A possible formula for is . Round the second answer to 3 decimal places.

(Short Answer)
4.7/5  (38)
(38)
Assume that all important features are shown in the following graph of .
What is ? For or , enter "inf" or "-inf".
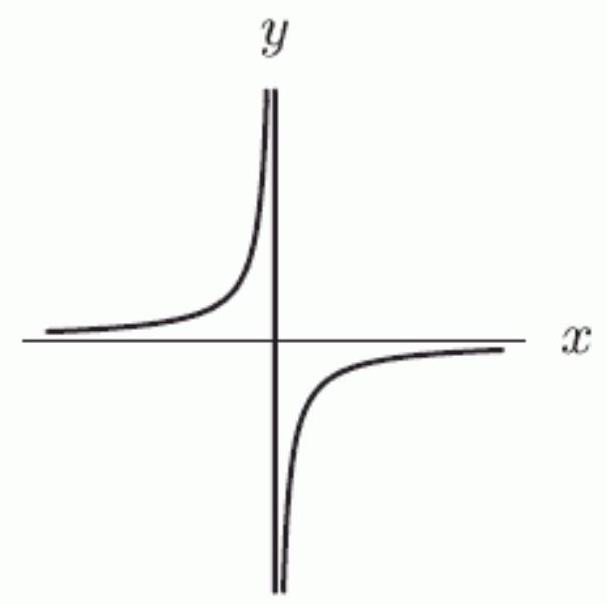
(Short Answer)
4.8/5  (43)
(43)
Let give the size of a population of animals in year . What will the population be after 12 years? Round to the nearest whole number.
(Short Answer)
4.9/5  (32)
(32)
The population of a city is increasing exponentially. In 2000 , the city had a population of 40,000 . In 2005 , the population was 58,502. The formula for , the population of the town years after 2000 , is given by .Round your second answer to 3 decimal places.
(Short Answer)
4.8/5  (37)
(37)
Let be the intersection of the graphs of the two exponential functions and , where . If is increased, does increase, decrease, or stay the same?
(Short Answer)
4.8/5  (35)
(35)
Kevin buys a new CD player for , and finds two years later when he wants to sell it that it is only worth . Assuming the value of the CD player decreases exponentially, the formula for , the value of the CD player after years, is given by . Round your second answer to 2 decimal places.
(Short Answer)
4.8/5  (38)
(38)
Is the formula for a function representing a quantity which begins at an amount larger than in year and grows at a continuous annual rate of given by ?
(True/False)
4.9/5  (38)
(38)
The populations of 4 species of animals are given by the following equations:
What is the largest initial population of the 4 species?
(Short Answer)
4.8/5  (39)
(39)
In the following figure, the functions , and can all be written in the form . Which one has the largest value for ?
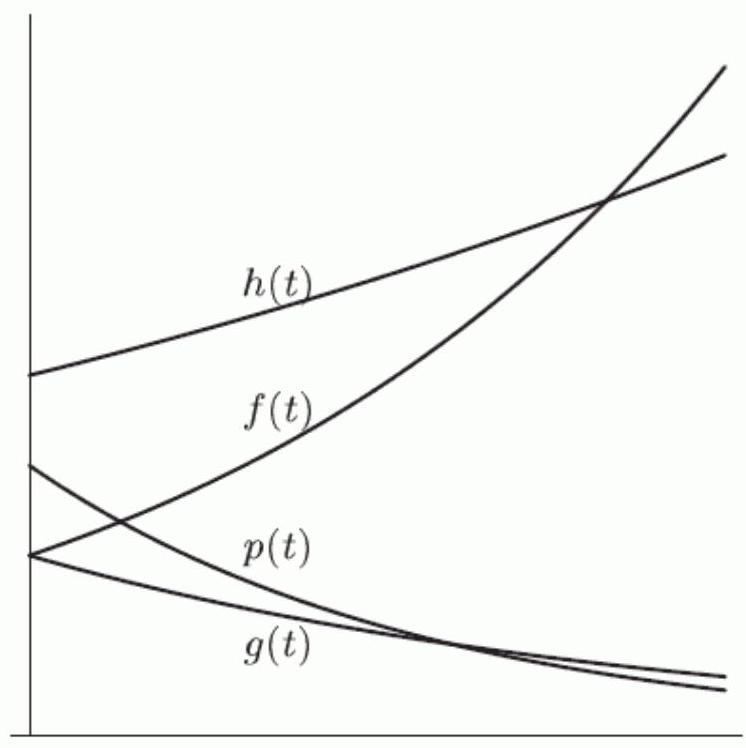
(Short Answer)
4.8/5  (34)
(34)
The following table gives values from an exponential or a linear function. Determine which, and find values for and so that if the function is linear, or if the function is exponential.
a= ---------------,b= ------------
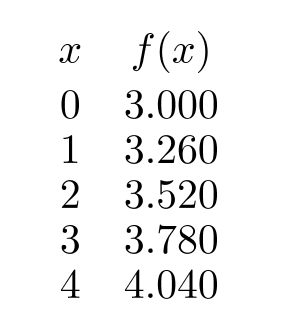
(Short Answer)
4.7/5  (41)
(41)
The graph below shows the quantity of a drug in a patient's bloodstream over a period of time , in minutes.
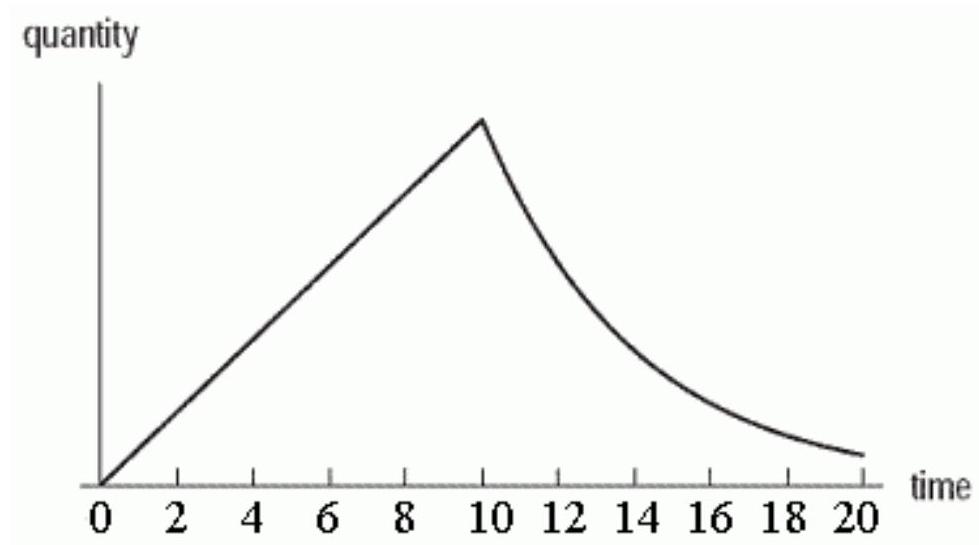 Which of the following scenarios best describes the graph?
Which of the following scenarios best describes the graph?
(Multiple Choice)
4.9/5  (35)
(35)
In 2006, the cost of a particular piece of computer equipment was and going down at a rate of per year. Assuming this percentage remains constant, what is the formula for , the cost of this equipment in dollars, as a function of , the number of years since 2006 ?
(Multiple Choice)
4.9/5  (43)
(43)
The price of an item increases due to inflation. Let give the price of the item as a function of time in years, with in 2004 . Estimate to 2 decimal places.
(Short Answer)
4.9/5  (33)
(33)
Let be given in the table below. Find the value of if is exponential.
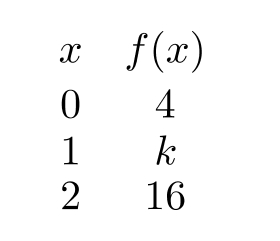
(Short Answer)
4.9/5  (40)
(40)
Write the formula for the price of a gallon of gas in days if the price is on day and the price increases by per day.
(Short Answer)
4.8/5  (37)
(37)
A biologist measures the amount of contaminant in a lake 2 hours after a chemical spill and again 11 hours after the spill. She sets up two possible models to determine , the amount of the chemical remaining in the lake as a function of , the time in hours since the spill. The first model assumes the contaminant is leaving the lake at a constant rate, which she determines to be 3 tons\hour. Using this model, she estimates that the lake will be free from the contaminant 20 hours after the spill. Thus, Q(2)= ---------- and Q(11)= ----------- The second model assumes that the amount of contaminant decreases exponentially. In this model, she finds that . Round both answers to 3 decimal places.
(Short Answer)
4.7/5  (30)
(30)
The graph of has a horizontal asymptote at ---------. (If there is no horizontal asymptote, enter "DNE".)
(Short Answer)
4.7/5  (30)
(30)
Showing 21 - 40 of 94
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)