Exam 4: Exponential Functions
Exam 1: Linear Functions and Change148 Questions
Exam 2: Functions138 Questions
Exam 3: Quadratic Functions46 Questions
Exam 4: Exponential Functions94 Questions
Exam 5: Logarithmic Functions87 Questions
Exam 6: Transformations of Functions and Their Graphs85 Questions
Exam 7: Trigonometry and Periodic Functions178 Questions
Exam 8: Triangle Trigonometry and Polar Coordinates43 Questions
Exam 9: Trigonometric Identities, Models, and Complex Numbers106 Questions
Exam 10: Compositions, Inverses, and Combinations of Functions69 Questions
Exam 11: Polynomial and Rational Functions145 Questions
Exam 12: Vectors and Matrices104 Questions
Exam 13: Sequences and Series81 Questions
Exam 14: Parametric Equations and Conic Sections128 Questions
Select questions type
An investment grows according to the formula . How many years will it take for the original investment to triple? Round to 1 decimal place.
(Short Answer)
4.7/5  (27)
(27)
Which of the following characteristics describe the graph of ?
(Multiple Choice)
4.8/5  (33)
(33)
Each of the functions in the table below is increasing, but each increases in a different way. One is linear, one is exponential, and one is neither.
 The following three graphs correspond with the functions in the table. Which is the graph of ?
The following three graphs correspond with the functions in the table. Which is the graph of ?
(Multiple Choice)
4.8/5  (36)
(36)
A population has size 3,000 at time , with in years. If the population grows by per year, what is the formula for , the population at time ?
(Multiple Choice)
4.9/5  (28)
(28)
If you start with , how much money will you have after a increase?
(Short Answer)
4.9/5  (39)
(39)
For the instantaneous compound interest in the formula , find the effective annual growth rate. Round to the nearest hundredth of a percent.
(Short Answer)
4.7/5  (24)
(24)
Which of the following is correctly ordered from least to greatest?
(Multiple Choice)
4.8/5  (37)
(37)
The amount of pollution in a harbor hours after it was contaminated by illegal dumping is given by tons. What percentage of the pollution leaves the harbor each hour?
(Short Answer)
4.7/5  (39)
(39)
The following figure gives the graph of , where is the computer hard disk capacity (in hundreds of megabytes) that could be bought for years past 1989 . If the trend displayed in the graph continued, how many megabytes would a hard drive have in 1997? Round to the nearest hundred.
, capacity (in 100 s of megabytes)
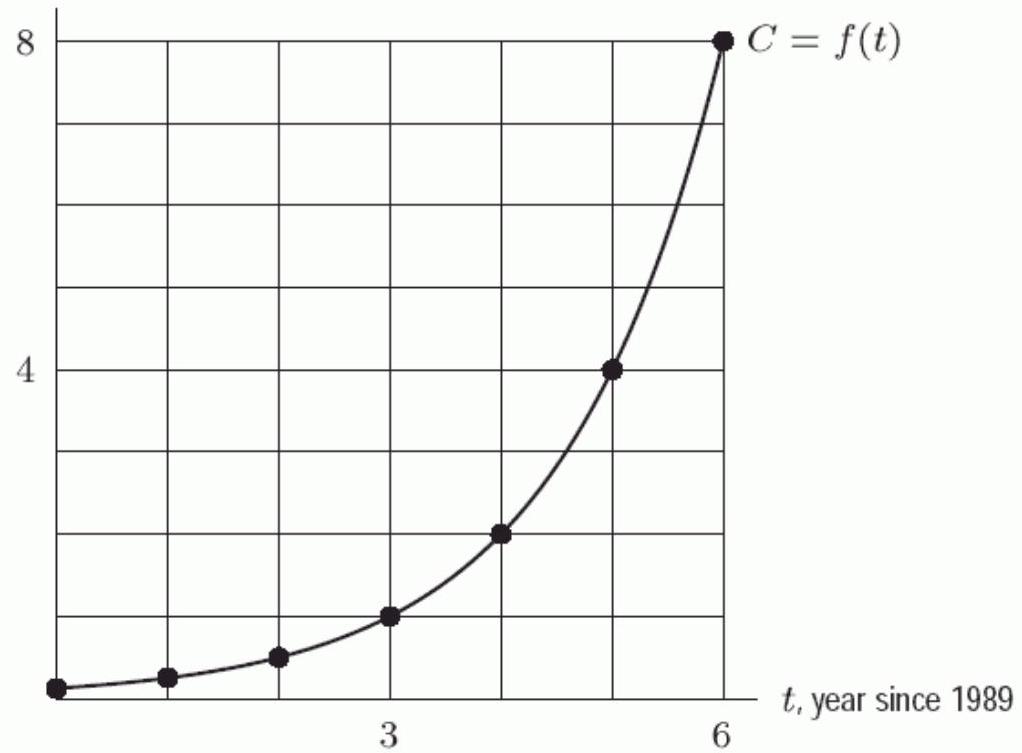
(Short Answer)
4.8/5  (34)
(34)
The population of a city has been growing at a rate of per year. If the population was 100,000 in 1990, what was the population in 1995? Round to the nearest whole number.
(Short Answer)
4.9/5  (40)
(40)
The population of a city is increasing exponentially. In 2000 , the city had a population of 70,000. In 2003, the population was 89,870 . Let be the population of the town years after 2000 . Use a graph of to estimate the year in which the population will reach 250,000 .
(Short Answer)
4.9/5  (30)
(30)
A store's sales of cassette tapes of music decreased by per year over a period of 5 years. By what total percent did sales of cassette tapes decrease over this time period? Round to 1 decimal place.
(Short Answer)
4.7/5  (33)
(33)
For the instantaneous compound interest in the formula , find the effective annual growth rate. Round to the nearest hundredth of a percent.
(Short Answer)
4.8/5  (38)
(38)
What is the maximum number of solutions the equation can have?
(Short Answer)
4.8/5  (34)
(34)
Is the formula for a function representing a quantity which begins at in year and grows at a continuous annual rate of given by
(True/False)
4.9/5  (33)
(33)
If you start with , how much money will you have after a increase followed by a decrease?
(Short Answer)
4.8/5  (34)
(34)
A population is 30,000 in year and declines at a continuous rate of per year. What is the formula for , the population in year ?
(Multiple Choice)
4.8/5  (40)
(40)
A radioactive substance decays by every year. Which of the following is the formula for the quantity, , of a 10 gram sample remaining after years?
(Multiple Choice)
4.7/5  (39)
(39)
Showing 41 - 60 of 94
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)