Exam 4: Exponential Functions
Exam 1: Linear Functions and Change148 Questions
Exam 2: Functions138 Questions
Exam 3: Quadratic Functions46 Questions
Exam 4: Exponential Functions94 Questions
Exam 5: Logarithmic Functions87 Questions
Exam 6: Transformations of Functions and Their Graphs85 Questions
Exam 7: Trigonometry and Periodic Functions178 Questions
Exam 8: Triangle Trigonometry and Polar Coordinates43 Questions
Exam 9: Trigonometric Identities, Models, and Complex Numbers106 Questions
Exam 10: Compositions, Inverses, and Combinations of Functions69 Questions
Exam 11: Polynomial and Rational Functions145 Questions
Exam 12: Vectors and Matrices104 Questions
Exam 13: Sequences and Series81 Questions
Exam 14: Parametric Equations and Conic Sections128 Questions
Select questions type
A population has size 3,500 at time , with in years. If the population grows by 80 people per year, what is the formula for , the population at time ?
(Multiple Choice)
4.7/5  (30)
(30)
Let give the size of a population of animals in year . After how many years will the population be approximately 10,099 ? Round to the nearest year.
(Short Answer)
4.8/5  (34)
(34)
Is the formula for a function representing a quantity which begins at in year and grows at a constant annual rate of given by
(True/False)
4.9/5  (38)
(38)
Find a possible formula for the exponential function such that the points and are on the graph.
(Short Answer)
4.9/5  (37)
(37)
Jeff has . He placed in Bank 1 with an account earning annual interest, compounded continuously. He also placed \$20,000 in Bank 2 with an account earning 3.6\% annual interest compounded weekly. After 10 years,
A) how much money is in Bank 1 ?
B) how much money is in Bank 2?
(Short Answer)
4.9/5  (37)
(37)
The amount of pollution in a harbor hours after it was contaminated by illegal dumping is given by tons. After how many hours is there less than 10 tons of pollution in the harbor? Round to 1 decimal place.
(Short Answer)
4.8/5  (27)
(27)
A biologist measures the amount of contaminant in a lake 3 hours after a chemical spill and again 11 hours after the spill. She sets up two possible models to determine , the amount of the chemical remaining in the lake as a function of , the time in hours since the spill. The first model assumes the contaminant is leaving the lake at a constant rate, which she determines to be 7 tons\hour. Using this model, she estimates that the lake will be free from the contaminant 24 hours after the spill. The second model assumes that the amount of contaminant decreases exponentially. She measures the spill a third time after 23 hours and finds that 44 tons remain. Which model seems best?
(Multiple Choice)
4.8/5  (30)
(30)
The following figure gives the graph of , where is the computer hard disk capacity (in hundreds of megabytes) that could be bought for years past 1989 . If the trend displayed in the graph continued, in what year would the capacity that can be bought for be 4,600 ?
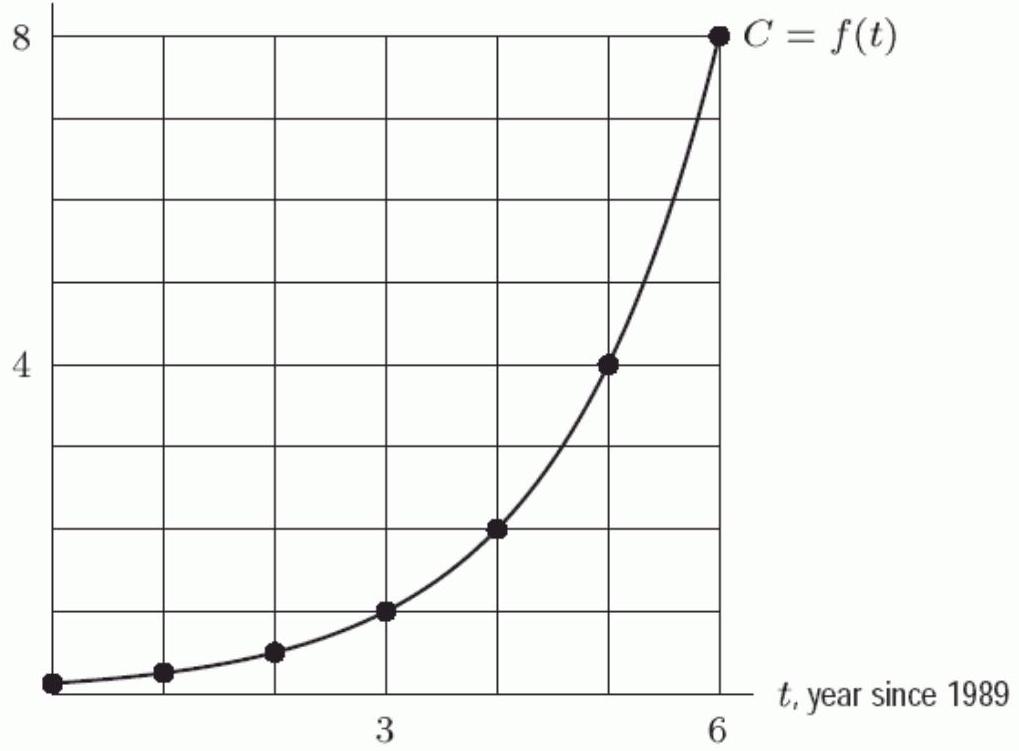
(Short Answer)
4.9/5  (34)
(34)
Each of the functions in the table below is increasing, but each increases in a different way. One is linear, one is exponential, and one is neither.
 The formula for the exponential one is Round your second answer to 2 decimal places.
The formula for the exponential one is Round your second answer to 2 decimal places.
(Short Answer)
4.8/5  (27)
(27)
The US population in 2005 was approximately 296.4 million. Assume the population increases at a rate of per year. Some demographers believe that the ideal population of the United States is about 130 million. According to this model, in what year did this occur?
(Short Answer)
4.8/5  (38)
(38)
A biologist measures the amount of contaminant in a lake 2 hours after a chemical spill and again 15 hours after the spill. She sets up a possible model to determine , the amount of the chemical remaining in the lake as a function of , the time in hours since the spill. The model assumes the contaminant is leaving the lake at a constant rate, which she determines to be 6 tons\hour. She estimates that the lake will be free from the contaminant 35 hours after the spill. How many tons of the contaminant were in the lake at the 15 hour reading?
(Short Answer)
4.9/5  (31)
(31)
An ant population grows at a continuous growth rate of . If the population starts with 22,000 ants, how many ants are there after 6 months? Round your answer to the nearest ant.
(Short Answer)
4.9/5  (40)
(40)
The price of an item increases due to inflation. Let give the price of the item as a function of time in years, with in 2004. What is the practical interpretation of ?
(Multiple Choice)
4.8/5  (30)
(30)
Showing 61 - 80 of 94
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)