Exam 8: Drawing Inferences From Large Samples
Exam 1: Introduction to Statistics17 Questions
Exam 2: Organization and Description of Data53 Questions
Exam 3: Descriptive Study of Bivariate Data44 Questions
Exam 4: Probability54 Questions
Exam 5: Probability Distributions49 Questions
Exam 6: The Normal Distribution32 Questions
Exam 7: Variation in Repeated Samplessampling Distributions31 Questions
Exam 8: Drawing Inferences From Large Samples48 Questions
Exam 9: Small Sample Inferences for Normal Populations36 Questions
Exam 10: Comparing Two Treatments37 Questions
Exam 11: Regression Analysis I29 Questions
Exam 12: Regression Analysis II Multiple Linear Regression and Other Topics5 Questions
Exam 13: Analysis of Categorical Data19 Questions
Exam 14: Analysis of Variance Anova16 Questions
Exam 15: Nonparametric Inference15 Questions
Select questions type
A parameter is a numerical feature of a probability distribution.
(True/False)
4.9/5  (29)
(29)
The baggage manager of an airport wants to improve the time that passengers wait in the baggage claim area. She has a sample of 129 domestic flights. The mean waiting time is = 12 minutes and s = 3.6 minutes. Is the claim that μ>13.5 minutes substantiated by these data? Test with α = 0.01.
(Essay)
4.9/5  (24)
(24)
Out of a sample of 500 students, 401 owned a smart phone that was less than 3 years old. Obtain the estimated standard error. Round your answer to three decimal places.
(Short Answer)
4.9/5  (38)
(38)
The research department of a biochemical industry took a sample of 60 bacteria cultures of the same kind and observed that the mean weight was 25.267 grams with standard deviation of 8.816 grams. Obtain a 99% confidence interval for the mean weight of the bacteria cultures.
(Short Answer)
5.0/5  (39)
(39)
The following summary of a data set refers to the girth of grizzly bears in centimenters.
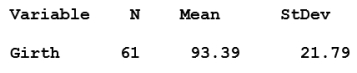 Find the 94% error margin. Round your answer to two decimal places.
Find the 94% error margin. Round your answer to two decimal places.
(Short Answer)
4.8/5  (40)
(40)
A survey is conducted of n = 957 adults (65 years or older) and x = 258 reported high blood pressure problems.
A) Provide a point estimate of p. Round your answer to three decimal places.
B) Determine the 96% error margin. Round your answer to four decimal places.
(Essay)
4.9/5  (37)
(37)
An inspection of eight wind turbines revealed that 13 operate too loudly according to new sound restrictions. The summary statistics are
n = 80 x = 13
Let p = population proportion that are too loud.
(a) Give a point estimate of p and its estimated standard error
(b) Obtain a 95 % confidence interval for the population mean p.
(c) Does your interval cover p? Explain.
(Essay)
4.7/5  (33)
(33)
Assuming the population is normal and is known, a 98% confidence interval for is given by
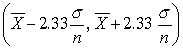
(True/False)
4.9/5  (35)
(35)
The number of times an undergraduate binge watched a TV se- ries in the past month was recorded for a sample of size 49. The summary statistics are
n = 49 = 2.1 s = 1.61
Let µ =population mean number of times.
(a) Conduct a test of hypotheses with the intent of showing that
µ > 1.5. Take α = .05.
(b) Calculate the P-value. Does this strengthen your conclusion to the test of hypotheses? Explain.
(c) Based on the conclusion to your test in Part a, what error could you have made.
(Essay)
4.9/5  (42)
(42)
When estimating the mean of a population, how large a sample is required in order that 96% error margin be of the population standard deviation?
(Short Answer)
4.9/5  (38)
(38)
When using to estimate μ , find the standard error for n = 160, σ =51 . Round your answer to three decimal places.
(Short Answer)
4.9/5  (32)
(32)
When estimating the mean of a population, how large a sample is required in order that the 94% error margin be 14% of the population standard deviation?
(Short Answer)
4.8/5  (29)
(29)
When using to estimate μ find the 100 (1-α)% error margin for
n = 146 σ =63 98% error margin.
Round your answer to three decimal places.
(Short Answer)
4.9/5  (41)
(41)
Given the standard deviation σ, the statement of your claim about μ , the sample size, and the desired level of significance α.
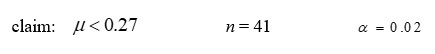 Formulate:
a) the hypotheses,
b) the test statistic Z,
c) the rejection region.
Formulate:
a) the hypotheses,
b) the test statistic Z,
c) the rejection region.
(Essay)
4.8/5  (33)
(33)
An industrial researcher wants to perform a test with the intent of establishing that this company's compact fluorescent lamp has a mean life greater than 7100 hours. The sample size is 128 and he knows that =79 hours.
Find the numerical value of c so that the test 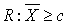 has a 5% level of significance.
has a 5% level of significance.
(Multiple Choice)
4.9/5  (38)
(38)
The number of times an undergraduate binge watched a TV se- ries in the past month was recorded for a sample of size 49. The summary statistics are
n = 49 = 2.1 s = 1.61
Let µ =population mean number of times.
(a) Give a point estimate of µ and its estimated standard error.
(b) Obtain a 95 % confidence interval for the population mean µ.
(c) Does your interval cover µ? Explain
(Essay)
4.8/5  (39)
(39)
Given the standard deviation σ, the statement of your claim about μ, the sample size, and the desired level of significance α.
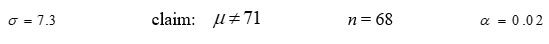 Formulate:
a) the hypotheses,
b) the test statistic Z,
c) the rejection region.
Formulate:
a) the hypotheses,
b) the test statistic Z,
c) the rejection region.
(Essay)
5.0/5  (36)
(36)
Assume n = 38, = 23.367, and s = 11.056. Obtain a 98% confidence interval for μ, the population mean.
(Short Answer)
4.8/5  (41)
(41)
Suppose = 4.55 and s = 5.17 for N = 40. We claim that H0 = 2.3 and H1 ≠ 2.3
. Find the P- value. Round your answer to four decimal places.
(Short Answer)
4.9/5  (34)
(34)
A random sample of 781 applicants for drivers license was taken, 270 of the applicants failed the driving test. Find a 90% confidence interval for the corresponding population proportion.
(Essay)
5.0/5  (38)
(38)
Showing 21 - 40 of 48
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)