Exam 17: Nonparametric Methods: Goodness-Of-Fit Tests

What is the lowest level of data for which the chi-square goodness-of-fit test is appropriate? ______________

A survey of the opinions of property owners about a street widening project was taken to determine whether the property owners' opinions were related to their property's distance (front-footage) from the street. A randomly selected sample of 100 property owners was contacted and the results are shown below. 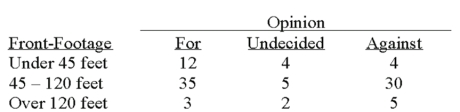At the 5% level of significance, what is the critical value?

We are interested in knowing if the following frequency distribution is normally distributed. The mean and standard deviation of the data is 600 and 160. 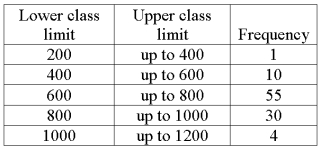If the distribution was normally distributed, what is expected frequency for the "400 up to 600" class?

What is the null hypothesis in the goodness-of-fit test? ____________

To determine if a set of ungrouped, raw data is normally distributed, what test statistic would we use?

In the goodness-of-fit test, the chi-square distribution is used to determine how well an observed distribution of observations "fits" an expected distribution of observations.

A survey of the opinions of property owners about a street widening project was taken to determine whether the resulting opinion was related to the distance from the street. A randomly selected sample of 100 property owners was contacted and the results are shown below. 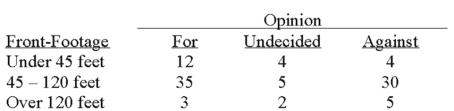What is the expected frequency for people who are in favor of the project and have less than 45 feet of property foot-frontage?

To test a hypothesis that a frequency distribution for sample data is normally distributed, class limits are transformed using a _____________.

A personnel manager is concerned about absenteeism. She decides to sample the records to determine if absenteeism is distributed evenly throughout the six-day workweek. The null hypothesis to be tested is: Absenteeism is distributed evenly throughout the week. The 0.01 level is to be used. The sample results are: What kind of frequencies are the numbers 12, 9, 11, 10, 9, and 9 called?

A Chi-square goodness-of-fit test is used to determine how well an observed distribution fits an __________ distribution.

We are interested in knowing if the following frequency distribution is normally distributed. The mean and standard deviation of the data is 600 and 160. 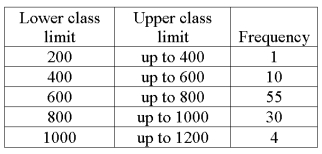What are the standard normal z-statistic class limits for the "800 up to 1000" class?

Nonparametric tests require no assumptions about the shape of the population distribution.

We are interested in knowing if the following frequency distribution is normally distributed. The mean and standard deviation of the data is 600 and 160. 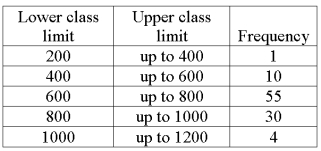To test the hypothesis that the frequency distribution is normally distributed, what is the value of the chi-square critical value at the .05 level of significance?

There is not one, but a family of chi-square distributions. There is a chi-square distribution for 1 degree of freedom, another for 2 degrees of freedom, another for 3 degrees of freedom, and so on.

For a contingency table, the expected frequency for a cell is found by dividing the row total by the grand total.

In a goodness-of-fit test, the null hypothesis (no difference between sets of observed and expected frequencies) is rejected when the

For people released from prison, the following table shows their adjustment to civilian life and place of residence. 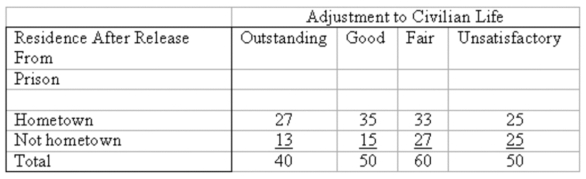What is the critical value for this contingency table at the 0.01 level of significance?

If the significance level for an Anderson-Darling test is 0.05 and the p-value is 0.001, the null hypothesis is rejected and we conclude that the data _________ normally distributed.

The shape of the chi-square distribution depends on the size of the sample.

A personnel manager is concerned about absenteeism. She decides to sample the records to determine if absenteeism is distributed evenly throughout the six-day workweek. The null hypothesis to be tested is: Absenteeism is distributed evenly throughout the week. The 0.01 level is to be used. The sample results are: What is the critical value of chi-square with $\alpha$ = 0.05?