Question 1

If the random variable X is exponentially distributed with parameter λ = 3,then the probability P(X ≥ 2)equals:

Accepted Answer

A) 0.3333 
B) 0.5000 
C) 0.6667 
D) 0.0025 
A) 0.3333 
B) 0.5000 
C) 0.6667 
D) 0.0025

Question 2

To find the probability for a uniform random variable you take the ____________________ times the ____________________ of its corresponding rectangle.

Accepted Answer

base; height
 height

Question 3

If the random variable X is exponentially distributed with parameter λ = 5,then the variance of X,σ2 = V(X)= 0.04.

Accepted Answer

A) True 
 B)False

Question 4

In the standard normal distribution,z0.05 = 1.645 means that 5% of all values of z are below 1.645 and 95% are above it.

Accepted Answer

A) True 
 B)False

Question 5

Suppose X has an exponential distribution with mean 2.Find f(x).

Accepted Answer

f(x)= 0.50

Question 6

The shape of a   2 distribution is ____________________.

Accepted Answer

positively

Question 7

Which of the following is always true for all probability density functions of continuous random variables?

Accepted Answer

A) The probability at any single point is zero. 
B) They contain an uncountable number of possible values. 
C) The total area under the density function f(x)equals 1. 
D) All of these choices are true. 
A) The probability at any single point is zero. 
B) They contain an uncountable number of possible values. 
C) The total area under the density function f(x)equals 1. 
D) All of these choices are true.

Question 8

The variance of a Student t distribution approaches zero as the degrees of freedom approaches infinity.

Accepted Answer

A) True 
 B)False

Question 9

The mean and variance of a 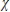  2 distribution approach ____________________ as the degrees of freedom increase.

Accepted Answer

Question 10

Truck Salesman 
A used truck salesman in a small town states that,on the average,it takes him 5 days to sell a truck.Assume that the probability distribution of the length of time between sales is exponentially distributed. ​ ​
-{Truck Salesman Narrative} What is the probability that he will have to wait at least 8 days before making another sale?

Accepted Answer

0.2019 (No

Question 11

A continuous random variable X has a uniform distribution between 5 and 15 (inclusive),then the probability that X falls between 10 and 20 is 1.0.

Accepted Answer

A) True 
 B)False

Question 12

For a continuous random variable,the probability for each individual value of X is ____________________.

Accepted Answer

The answer of For a continuous random variable,the probability for...

Question 13

Subway Waiting Time 
At a subway station the waiting time for a subway is found to be uniformly distributed between 1 and 5 minutes. ​ ​
-{Subway Waiting Time Narrative} What is the probability density function for this uniform distribution?

Accepted Answer

The answer of Subway Waiting Time 
At a subway station...

Question 14

Subway Waiting Time 
At a subway station the waiting time for a subway is found to be uniformly distributed between 1 and 5 minutes. ​ ​
-{Subway Waiting Time Narrative} What is the probability that the subway arrives in the first minute and a half?

Accepted Answer

The answer of Subway Waiting Time 
At a subway station...

Question 15

The time required to complete a particular assembly operation has a uniform distribution between 25 and 50 minutes.
a.What is the probability density function for this uniform distribution?
b.What is the probability that the assembly operation will require more than 40 minutes to complete?
c.Suppose more time was allowed to complete the operation,and the values of X were extended to the range from 25 to 60 minutes.What would f(x)be in this case?

Accepted Answer

a. f(x)= 1/25,25 ≤ x

Question 16

What happens to the shape,mean,and variance of a Student t distribution as the degrees of freedom increase?

Accepted Answer

As the degrees of freedom of t

Question 17

Use the F table to find the following probabilities.
a.P(F6,14 > 2.85)
b.P(F20,60 > 2.20)
c.P(F12,25 > 2.51)
d.P(F15,30 > 2.01)

Accepted Answer

a. 0.05 
b

Question 18

Probability for continuous random variables is found by finding the ____________________ under a curve.

Accepted Answer

The answer of Probability for continuous random variables is found...

Question 19

If the random variable X is exponentially distributed with parameter λ = 4,then the probability P(X ≤ 0.25),up to 4 decimal places,is

Accepted Answer

A) 0.6321 
B) 0.3679 
C) 0.2500 
D) None of these choices. 
A) 0.6321 
B) 0.3679 
C) 0.2500 
D) None of these choices.

Question 20

What number corresponds to t0.05,10?

Accepted Answer

A) 1.812 
B) 1.372 
C) 2.228 
D) 1.833 
A) 1.812 
B) 1.372 
C) 2.228 
D) 1.833

Exam 8: Continuous Probability Distributions

If the random variable X is exponentially distributed with parameter λ = 3,then the probability P(X ≥ 2)equals:

To find the probability for a uniform random variable you take the ____________________ times the ____________________ of its corresponding rectangle.

If the random variable X is exponentially distributed with parameter λ = 5,then the variance of X,σ2 = V(X)= 0.04.

In the standard normal distribution,z0.05 = 1.645 means that 5% of all values of z are below 1.645 and 95% are above it.

Suppose X has an exponential distribution with mean 2.Find f(x).

The shape of a 2 distribution is ____________________.

Which of the following is always true for all probability density functions of continuous random variables?

The variance of a Student t distribution approaches zero as the degrees of freedom approaches infinity.

The mean and variance of a 2 distribution approach ____________________ as the degrees of freedom increase.

A continuous random variable X has a uniform distribution between 5 and 15 (inclusive),then the probability that X falls between 10 and 20 is 1.0.

For a continuous random variable,the probability for each individual value of X is ____________________.

Subway Waiting Time At a subway station the waiting time for a subway is found to be uniformly distributed between 1 and 5 minutes. ​ ​ -{Subway Waiting Time Narrative} What is the probability density function for this uniform distribution?

Subway Waiting Time At a subway station the waiting time for a subway is found to be uniformly distributed between 1 and 5 minutes. ​ ​ -{Subway Waiting Time Narrative} What is the probability that the subway arrives in the first minute and a half?

What happens to the shape,mean,and variance of a Student t distribution as the degrees of freedom increase?

Use the F table to find the following probabilities. a.P(F6,14 > 2.85) b.P(F20,60 > 2.20) c.P(F12,25 > 2.51) d.P(F15,30 > 2.01)

Probability for continuous random variables is found by finding the ____________________ under a curve.

If the random variable X is exponentially distributed with parameter λ = 4,then the probability P(X ≤ 0.25),up to 4 decimal places,is

What number corresponds to t0.05,10?

What Is Statistics

Graphical Descriptive Techniques 1

Graphical Descriptive Techniques 2

Numerical Descriptive Techniques

Data Collection and Sampling

Probability

Random Variables and Discrete Probability Distributions

Sampling Distributions

Introduction to Estimation

Introduction to Hypothesis Testing

Inference About a Population

Inference About Comparing Two Populations

Analysis of Variance

Chi-Squared Tests

Simple Linear Regression and Correlation

Multiple Regression

Model Building

Nonparametric Statistics

Time-Series Analytics and Forecasting

Statistical Process Control

Decision Analysis

Conclusion

Filters

To find the probability for a uniform random variable you take the times the of its corresponding rectangle.

If the random variable X is exponentially distributed with parameter λ = 5,then the variance of X,σ² = V(X)= 0.04.

In the standard normal distribution,z_0.05 = 1.645 means that 5% of all values of z are below 1.645 and 95% are above it.

The shape of a ² distribution is ____________________.

The mean and variance of a ² distribution approach ____________________ as the degrees of freedom increase.

Subway Waiting Time At a subway station the waiting time for a subway is found to be uniformly distributed between 1 and 5 minutes. -{Subway Waiting Time Narrative} What is the probability density function for this uniform distribution?

Subway Waiting Time At a subway station the waiting time for a subway is found to be uniformly distributed between 1 and 5 minutes. -{Subway Waiting Time Narrative} What is the probability that the subway arrives in the first minute and a half?

Use the F table to find the following probabilities. a.P(F_6,14 > 2.85) b.P(F_20,60 > 2.20) c.P(F_12,25 > 2.51) d.P(F_15,30 > 2.01)

What number corresponds to t_0.05,10?