Exam 40: Quantum Mechanics
Exam 1: Units,physical Quantities,and Vectors107 Questions
Exam 2: Motion Along a Straight Line59 Questions
Exam 3: Motion in Two or Three Dimensions50 Questions
Exam 4: Newtons Laws of Motion44 Questions
Exam 5: Applying Newtons Laws95 Questions
Exam 6: Work and Kinetic Energy54 Questions
Exam 7: Potential Energy and Energy Conservation55 Questions
Exam 8: Momentum,impulse,and Collisions50 Questions
Exam 9: Rotation of Rigid Bodies26 Questions
Exam 10: Dynamics of Rotational Motion49 Questions
Exam 11: Equilibrium and Elasticity50 Questions
Exam 12: Fluid Mechanics50 Questions
Exam 13: Gravitation50 Questions
Exam 14: Periodic Motion50 Questions
Exam 15: Mechanical Waves44 Questions
Exam 16: Sound and Hearing65 Questions
Exam 17: Temperature and Heat63 Questions
Exam 18: Thermal Properties of Matter58 Questions
Exam 19: The First Law of Thermodynamics52 Questions
Exam 20: The Second Law of Thermodynamics50 Questions
Exam 21: Electric Charge and Electric Field60 Questions
Exam 22: Gausss Law41 Questions
Exam 23: Electric Potential55 Questions
Exam 24: Capacitance and Dielectrics52 Questions
Exam 25: Current,resistance,and Electromotive Force55 Questions
Exam 26: Direct-Current Circuits53 Questions
Exam 27: Magnetic Field and Magnetic Forces42 Questions
Exam 28: Sources of Magnetic Field52 Questions
Exam 29: Electromagnetic Induction39 Questions
Exam 30: Inductance27 Questions
Exam 31: Alternating Current50 Questions
Exam 32: Electromagnetic Waves47 Questions
Exam 33: The Nature and Propagation of Light28 Questions
Exam 34: Geometric Optics81 Questions
Exam 35: Interference33 Questions
Exam 36: Diffraction49 Questions
Exam 37: Relativity51 Questions
Exam 38: Photons: Light Waves Behaving As Particles38 Questions
Exam 39: Particles Behaving As Waves52 Questions
Exam 40: Quantum Mechanics43 Questions
Exam 41: Atomic Structure53 Questions
Exam 42: Molecules and Condensed Matter31 Questions
Exam 43: Nuclear Physics90 Questions
Exam 44: Particle Physics and Cosmology54 Questions
Select questions type
A 10.0-g bouncy ball is confined in a 8.3-cm-long box (an infinite well).If we model the ball as a point particle,what is the minimum kinetic energy of the ball? 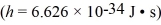
Free
(Multiple Choice)
4.9/5  (39)
(39)
Correct Answer:
A
A lithium atom,mass 1.17 × 10-26 kg,vibrates with simple harmonic motion in a crystal lattice,where the effective force constant of the forces on the atom is k = 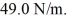
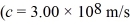 ,h = 6.626 × 10-34 J • s,h = 1.055 × 10-34 J • s,
,h = 6.626 × 10-34 J • s,h = 1.055 × 10-34 J • s, 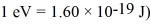 (a)What is the ground state energy of this system,in eV?
(b)What is the wavelength of the photon that could excite this system from the ground state to the first excited state?
(a)What is the ground state energy of this system,in eV?
(b)What is the wavelength of the photon that could excite this system from the ground state to the first excited state?
Free
(Short Answer)
4.9/5  (31)
(31)
Correct Answer:
(a)2.14 × 10-2 eV
(b)2.91 × 10-5 m
A particle trapped in a one-dimensional finite potential well with U0 = 0 in the region 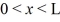 ,and finite U0 everywhere else,has a ground state wavenumber,k.The ground state wavenumber for the same particle in an infinite one-dimensional potential well of width L,would be
,and finite U0 everywhere else,has a ground state wavenumber,k.The ground state wavenumber for the same particle in an infinite one-dimensional potential well of width L,would be
Free
(Multiple Choice)
4.9/5  (31)
(31)
Correct Answer:
B
An 80-eV electron impinges upon a potential barrier 100 eV high and 0.20 nm thick.What is the probability the electron will tunnel through the barrier? (1 eV = 1.60 × 10-19 J, 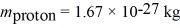 ,h = 1.055 × 10-34 J • s,h = 6.626 × 10-34 J • s)
,h = 1.055 × 10-34 J • s,h = 6.626 × 10-34 J • s)
(Multiple Choice)
4.7/5  (33)
(33)
An electron is confined in a harmonic oscillator potential well.What is the longest wavelength of light that the electron can absorb if the net force on the electron behaves as though it has a spring constant of 74 N/m? (mel = 9.11 × 10-31 kg,c = 3.00 × 108 m/s, 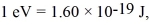 h = 1.055 × 10-34 J • s,h = 6.626 × 10-34 J • s)
h = 1.055 × 10-34 J • s,h = 6.626 × 10-34 J • s)
(Multiple Choice)
4.9/5  (36)
(36)
The wave function for an electron that is confined to x ≥ 0 nm is
ψ(x)= 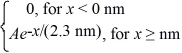 (a)What must be the value of A?
(b)What is the probability of finding the electron in the interval 1.15 nm ≤ x ≤ 1.84 nm?
(a)What must be the value of A?
(b)What is the probability of finding the electron in the interval 1.15 nm ≤ x ≤ 1.84 nm?
(Short Answer)
4.9/5  (32)
(32)
An electron is bound in an infinite square-well potential (a box)on the x-axis.The width of the well is L and the well extends from x = 0.00 nm to 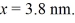 In its present state,the normalized wave function of the electron is given by: ψ(x)=
In its present state,the normalized wave function of the electron is given by: ψ(x)= 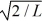 sin (2πx/L).What is the energy of the electron in this state?(h = 6.626 × 10-34 J • s,mel = 9.11 × 10-31 kg,
sin (2πx/L).What is the energy of the electron in this state?(h = 6.626 × 10-34 J • s,mel = 9.11 × 10-31 kg, 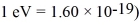
(Multiple Choice)
4.7/5  (41)
(41)
A particle confined in a rigid one-dimensional box (an infinite well)of length 17.0 fm has an energy level 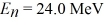 and an adjacent energy level En+1 = 37.5 MeV.What is the value of the ground state energy? (1 eV = 1.60 × 10-19 J)
and an adjacent energy level En+1 = 37.5 MeV.What is the value of the ground state energy? (1 eV = 1.60 × 10-19 J)
(Multiple Choice)
4.8/5  (39)
(39)
An electron is bound in an infinite well (a box)of width 0.10 nm.If the electron is initially in the n = 8 state and falls to the n = 7 state,find the wavelength of the emitted photon. 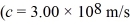 ,h = 6.626 × 10-34 J ∙ s,mel = 9.11 × 10-31 kg)
,h = 6.626 × 10-34 J ∙ s,mel = 9.11 × 10-31 kg)
(Short Answer)
4.8/5  (38)
(38)
One fairly crude method of determining the size of a molecule is to treat the molecule as an infinite square well (a box)with an electron trapped inside,and to measure the wavelengths of emitted photons.If the photon emitted during the n = 2 to n = 1 transition has wavelength 1940 nm,what is the width of the molecule? (c = 3.00 × 108 m/s, 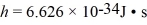 ,
, 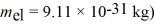
(Multiple Choice)
4.8/5  (29)
(29)
An electron is in the ground state of an infinite well (a box)where its energy is 5.00 eV.In the next higher level,what would its energy be? (1 eV = 1.60 × 10-19 J)
(Multiple Choice)
4.8/5  (32)
(32)
A set of five possible wave functions is given below,where L is a positive real number. ψ1(x)= Ae-x,for all x ψ2(x)= A cos x,for all x
Ψ3(x)=  ψ4(x)=
ψ4(x)= 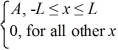 ψ5(x)=
ψ5(x)= 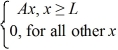 Which of the five possible wave functions are normalizable? (There may be more than one correct choice.)
Which of the five possible wave functions are normalizable? (There may be more than one correct choice.)
(Multiple Choice)
4.8/5  (37)
(37)
The energy of a particle in the second EXCITED state of a harmonic oscillator potential is 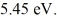 What is the classical angular frequency of oscillation of this particle?
What is the classical angular frequency of oscillation of this particle? 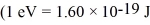 ,h = 1.055 × 10-34 J • s,h = 6.626 × 10-34 J • s)
,h = 1.055 × 10-34 J • s,h = 6.626 × 10-34 J • s)
(Multiple Choice)
5.0/5  (30)
(30)
The probability density for an electron that has passed through an experimental apparatus is shown in the figure.If 4100 electrons pass through the apparatus,what is the expected number that will land in a 0.10 mm-wide strip centered at x = 0.00 mm? 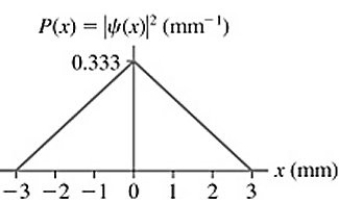
(Multiple Choice)
4.9/5  (36)
(36)
An electron with kinetic energy 2.80 eV encounters a potential barrier of height 4.70 eV.If the barrier width is 0.40 nm,what is the probability that the electron will tunnel through the barrier? (1 eV = 1.60 × 10-19 J,mel = 9.11 × 10-31 kg,h = 6.626 × 10-34 J • s)
(Multiple Choice)
5.0/5  (37)
(37)
A particle is confined to a one-dimensional box (an infinite well)on the x-axis between 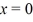 and
and 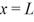 .The potential height of the walls of the box is infinite.The normalized wave function of the particle,which is in the ground state,is given by ψ(x)=
.The potential height of the walls of the box is infinite.The normalized wave function of the particle,which is in the ground state,is given by ψ(x)= 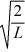 sin
sin 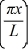 ,with
,with 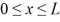 .What is the maximum probability per unit length of finding the particle?
.What is the maximum probability per unit length of finding the particle?
(Multiple Choice)
4.8/5  (32)
(32)
A one-dimensional finite potential well has potential energy U0 = 0 in the region 0 < x < .2 nm,and 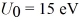 everywhere else.A particle with which of the energies listed below would be localized (trapped)within the potential well? (Select all correct answers.)
everywhere else.A particle with which of the energies listed below would be localized (trapped)within the potential well? (Select all correct answers.)
(Multiple Choice)
4.8/5  (32)
(32)
The lowest energy level of a particle confined to a one-dimensional region of space (a box,or infinite well)with fixed length L is E0.If an identical particle is confined to a similar region with fixed length L/6,what is the energy of the lowest energy level that the particles have in common? Express your answer in terms of E0.
(Short Answer)
4.9/5  (23)
(23)
Showing 1 - 20 of 43
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)