Exam 12: Simple Linear Regression
Exam 1: Data and Statistics104 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Presentations65 Questions
Exam 3: Descriptive Statistics: Numerical Measures162 Questions
Exam 4: Introduction to Probability146 Questions
Exam 5: Discrete Probability Distributions121 Questions
Exam 6: Continuous Probability Distributions165 Questions
Exam 7: Sampling and Sampling Distributions131 Questions
Exam 8: Interval Estimation131 Questions
Exam 9: Hypothesis Tests136 Questions
Exam 10: Comparisons Involving Means, Experimental Design and Analysis of Variance208 Questions
Exam 11: Comparisons Involving Proportions and a Test of Independence94 Questions
Exam 12: Simple Linear Regression140 Questions
Exam 13: Multiple Regression146 Questions
Select questions type
Part of an Excel output relating X (independent variable) and Y (dependent variable) is shown below. Fill in all the blanks marked with "?".

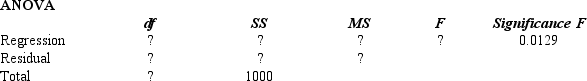
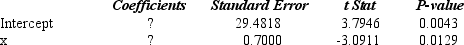
(Essay)
4.8/5  (30)
(30)
Exhibit 12-9
A regression and correlation analysis resulted in the following information regarding a dependent variable (y) and an independent variable (x).
 -Refer to Exhibit 12-9. The least squares estimate of b0 equals
-Refer to Exhibit 12-9. The least squares estimate of b0 equals
(Multiple Choice)
4.8/5  (31)
(31)
Exhibit 12-4
Regression analysis was applied between sales data (Y in $1,000s) and advertising data (x in $100s) and the following information was obtained.
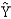 = 12 + 1.8 x
n = 17
SSR = 225
SSE = 75
Sb1 = 0.2683
-Refer to Exhibit 12-4. The t statistic for testing the significance of the slope is
= 12 + 1.8 x
n = 17
SSR = 225
SSE = 75
Sb1 = 0.2683
-Refer to Exhibit 12-4. The t statistic for testing the significance of the slope is
(Multiple Choice)
4.9/5  (42)
(42)
Exhibit 12-4
Regression analysis was applied between sales data (Y in $1,000s) and advertising data (x in $100s) and the following information was obtained.
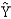 = 12 + 1.8 x
n = 17
SSR = 225
SSE = 75
Sb1 = 0.2683
-Refer to Exhibit 12-4. The critical t value for testing the significance of the slope at 95% confidence is
= 12 + 1.8 x
n = 17
SSR = 225
SSE = 75
Sb1 = 0.2683
-Refer to Exhibit 12-4. The critical t value for testing the significance of the slope at 95% confidence is
(Multiple Choice)
4.9/5  (29)
(29)
If the coefficient of determination is 0.81, the coefficient of correlation
(Multiple Choice)
4.7/5  (27)
(27)
Exhibit 12-3
You are given the following information about y and x.
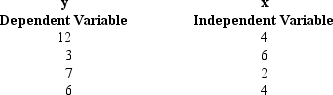 -Refer to Exhibit 12-3. The sample correlation coefficient equals
-Refer to Exhibit 12-3. The sample correlation coefficient equals
(Multiple Choice)
4.9/5  (42)
(42)
Exhibit 12-2
You are given the following information about y and x.
 -Refer to Exhibit 12-2. The point estimate of y when x = 10 is
-Refer to Exhibit 12-2. The point estimate of y when x = 10 is
(Multiple Choice)
4.8/5  (31)
(31)
Exhibit 12-1
The following information regarding a dependent variable (Y) and an independent variable (X) is provided. 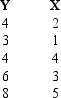 SSE = 6
SST = 16
-Refer to Exhibit 12-1. The MSE is
SSE = 6
SST = 16
-Refer to Exhibit 12-1. The MSE is
(Multiple Choice)
5.0/5  (43)
(43)
Below you are given information on annual income and years of college education.
 a.Develop the least squares regression equation.
b.Estimate the yearly income of an individual with 6 years of college education.
c.Compute the coefficient of determination.
d.Use a t test to determine whether the slope is significantly different from zero. Let = 0.05.
e. At 95% confidence, perform an F test and determine whether or not the model is significant.
a.Develop the least squares regression equation.
b.Estimate the yearly income of an individual with 6 years of college education.
c.Compute the coefficient of determination.
d.Use a t test to determine whether the slope is significantly different from zero. Let = 0.05.
e. At 95% confidence, perform an F test and determine whether or not the model is significant.
(Essay)
4.9/5  (34)
(34)
If the coefficient of correlation is a positive value, then
(Multiple Choice)
4.8/5  (35)
(35)
If the coefficient of correlation is -0.4, then the slope of the regression line
(Multiple Choice)
4.9/5  (32)
(32)
Compared to the confidence interval estimate for a particular value of y (in a linear regression model), the interval estimate for an average value of y will be
(Multiple Choice)
4.9/5  (36)
(36)
Regression analysis was applied between sales (in $10,000) and advertising (in $100) and the following regression function was obtained.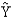 = 50 + 8 X
Based on the above estimated regression line if advertising is $1,000, then the point estimate for sales (in dollars) is
= 50 + 8 X
Based on the above estimated regression line if advertising is $1,000, then the point estimate for sales (in dollars) is
(Multiple Choice)
4.8/5  (28)
(28)
Regression analysis was applied between sales (in $1000) and advertising (in $100) and the following regression function was obtained. 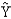 = 500 + 4 X
Based on the above estimated regression line if advertising is $10,000, then the point estimate for sales (in dollars) is
= 500 + 4 X
Based on the above estimated regression line if advertising is $10,000, then the point estimate for sales (in dollars) is
(Multiple Choice)
4.7/5  (40)
(40)
Below you are given a partial computer output based on a sample of 8 observations, relating an independent variable (x) and a dependent variable (y).

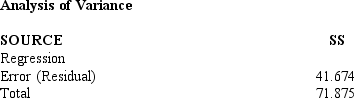 a.Develop the estimated regression line.
b.At = 0.05, test for the significance of the slope.
c.At = 0.05, perform an F test.
d.Determine the coefficient of determination.
a.Develop the estimated regression line.
b.At = 0.05, test for the significance of the slope.
c.At = 0.05, perform an F test.
d.Determine the coefficient of determination.
(Essay)
4.8/5  (35)
(35)
If there is a very weak correlation between two variables, then the coefficient of determination must be
(Multiple Choice)
4.7/5  (33)
(33)
Exhibit 12-8
The following information regarding a dependent variable Y and an independent variable X is provided
 -Refer to Exhibit 12-8. The Y intercept is
-Refer to Exhibit 12-8. The Y intercept is
(Multiple Choice)
4.7/5  (38)
(38)
If the coefficient of correlation is 0.90, then the coefficient of determination
(Multiple Choice)
4.8/5  (34)
(34)
If there is a very strong correlation between two variables then the coefficient of determination must be
(Multiple Choice)
4.9/5  (34)
(34)
Showing 121 - 140 of 140
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)