Exam 17: Appendix: Modeling Using Linear Programming

The constraint that requires the ending inventory from previous month plus current production minus ending inventory of this month equals this month's demand is known as a demand requirement.

Which of the following is generally TRUE of the transportation problem of linear programming?

The Pacific Computer Company makes two models of notebook personal computers: Model 410 with CD-ROM drive, and Model 540 with DVD drive. Profits on each model are $100 and $150, respectively. Weekly manufacturing data (in minutes) are given below: Notebook Dept. A Dept. B Model Manuf. Time Manuf. Time Assembly Time 410 5 14 25 540 10 7 40 Manufacturing time available in department A for the coming week is 300 minutes, and for department B, it is 420 minutes. Total time available during the week to assemble the fabricated units is 1600 minutes. a. What is the objective function if the company wants to maximize profits? b. What is the constraint corresponding to Department A assuming x₁ corresponds to Model 410? c. What is the optimum solution point for this problem? d. What is the maximum possible total profit?

If a company has a demand of 1,600 units for the month of May and a beginning of 900 units, and if X_m = production in May and L_m = the number of lost sales in May, which of the following equations represents the material-balance constraint?

A cement company has three factories that they identify as Alpha, Beta, and Gamma. They supply cement to three warehouses referred to as X, Y, and Z. The company wants to determine how much cement should be shipped from each factory to each warehouse to minimize shipping costs. The cost to ship each 100-pound bag, along with warehouse requirements and factory capacities in bags are shown in the table below: Warehouses Factories X Y Z Capacities (bags) Alpha \ .40 \ .60 \ .78 10,000 Beta 0.65 0.78 0.59 9,000 Gamma 0.56 0.61 0.71 7,000 Requirements (bags) 10,000 5,000 10,000 a. How many decision variables are there in this problem? b. What is (are) the constraint(s) corresponding to factory Alpha? c. How many constraints are required for this problem?

Since price is usually set by market conditions, the blending problem's use of linear programming attempts to meet the demand at a minimum cost.

Explain the essence of a transportation problem.

The constraint x₁ and x₂ $\ge$ 0 refers to:

A clothing distributor has four warehouses that serve four large cities. Each warehouse has a monthly capacity of 5,000 blue jeans. They are considering using a transportation LP approach to match demand and capacity. The following table provides data on their shipping cost, capacity, and demand constraints on a per-month basis: Warehouse City E City F City G City H A 0.53 0.21 0.52 0.41 B 0.31 0.38 0.41 0.29 C 0.56 0.32 0.54 0.33 D 0.42 0.55 0.34 0.52 City demand 2.000 3,000 3,500 5,500 a. How many variables are there in this formulation? b. How many constraints are involved in this problem? c. What is the constraint corresponding to City F?

A company manufactures 50-inch and 75-inch rear projection television sets. Each 50-inch set contributes $200 to profits and each 75-inch set contributes $475 to profits. The company has purchase commitments for 500 50-inch sets and 200 75-inch sets for the next month, so they want to make at least that many television sets. Although they think they can sell all the 50-inch sets that they could currently make, they do not think they can sell more than 375 75-inch sets. Their production capacity allows them to make only 975 sets in total including both types of television sets. They want to know how many of each type to make so as to maximize profits. a. What is the objective function for this LP problem? b. What are the constraints involving x₁, assuming that x₁ corresponds to 50-inch TV sets? c. What is the optimal solution point for this problem? d. What is the optimal value of the objective function?

Excel Solver can handle basic linear programming but not the special transportation problem.

A cargo airline company in South America ferries materials from four different airfields in Brazil (called A, B, C, and D) to two different airfields in Peru (numbered 1 and 2). Distances in hundreds of miles between the six different airfields are as shown below: Brazil Peru A B C D 1 2 6 17 5 2 12 8 12 9 Capacities 60 40 75 55 Requirements for airfield 1 are 140 tons per year and 80 tons per year for airfield 2. The president of the airlines wants to determine how much material should be shipped from each airfield in Brazil to each airfield in Peru so as to minimize total travel distance. a. How many decision variables are there in this problem? b. What is the constraint corresponding to airfield 1? c. What is the constraint corresponding to airfield B?

The Alpha Beta Corporation makes laser and inkjet printers for personal computers. Each laser printer yields $40.00 in profits and each ink jet printer provides $20.00. Each of the printers goes through two assembly areas. The following table provides processing times per unit (in minutes) as well as total available processing times per department: Printer Dept. A Dept. B Laser 9 12 Inkjet 6 8 Total time per day 216 384 Sales commitments require at least 5 laser printers and 10 inkjet printers to be made per day. The company is interested in determining how many of each printer to produce so as to maximize its profit. a. What is the objective function for this LP problem? b. What are the constraints corresponding to Dept. A if x₁ corresponds to laser printers? c. What are the optimal solution points for this problem? d. What is the optimal value of the objective function?

Given the partial project network below and the fact that F can be crashed three times if x_t = start time of Activity i, and y_i = amount of crash time used for Activity i. 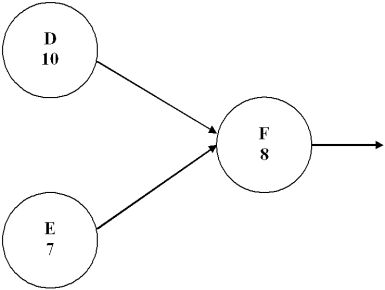a. Which of the following is correct? x_F $\ge$ x_D + 10 - y_D or x_F $\ge$ x_E + 10 + y_E or y_D, y_E $\le$ 0 or x_F -x_D - x_E + 10 $\ge$ 3 b. Which of the following is correct? y_D $\le$ 3 or y_E $\le$ 3 or y_F = y_D + y_E or y_F $\le$ 3

A company is considering a rate change, either an increase or a decrease in production, where X_t = production in a time period; R_t = increase in production rate from Period t−1 to Period t; D_t = decrease in production rate from Period t−1 to Period t. Which of the following is correct?

If Activity C directly precedes both D and E on a project network, and C can be crashed three (3) times using linear programming, then:

Constant terms in the objective function are called objective function _____.

A food processing company makes meatloaf to be sold in the frozen food section of supermarkets.Each week, the recipe used changes based on the current cost of ingredients. Ingredients and current costs are as shown below: Ingredient Cost/pound pork \ 2.87 hamburger \ 1.63 wheat filler \ 0.22 corn filler \ 0.16 For each batch made, at least 300 pounds of pork and 100 pounds of hamburger are required. No more than 200 pounds of wheat filler can be used per batch, and the amount of corn filler has to range between 50 and 150 pounds. Moreover, each batch must contain at least 500 pounds of meat and no more than 200 pounds of filler. a. What is the objective function if the company seeks to minimize costs? b. If x₁ is the amount of pork used, what are the constraints associated with it? c. If x₃ is the amount of wheat filler used, what are the constraints associated with it?

A small lumber company produces two types of pine boards used in home construction: 2x4s and 2x6s (dimensions in inches). It is attempting to determine how many of each to produce so as to minimize its costs on a per-minute basis. It has sales commitments to produce four 2x4s and two 2x6s per minute, but the management thinks they should not produce any more than eight 2x6s because of market demand. The company is also trying to support the community by employing people. Thus, it wants to keep at least 12 men employed, but only needs 2 men to produce each 2x4 and 1 person to produce each 2x6 per minute. It costs the company $.50 to produce a 2x4 and $.80 to produce a 2x6 per minute. a. What is the objective function for this LP problem? b. What is the constraint for the employment issue, assuming x₁ corresponds to 2x4s? c. What is the optimal solution point for this problem? d. What is the optimal value of the objective function?

In production scheduling, (ending inventory from the previous month) + (current production)-(ending inventory this month) = _____.