Question 1

When automatically running multiple optimizations in Analytic Solver Platform,what spreadsheet function indicates which optimization is being run?

Accepted Answer

A) =PsiOptNum) 
B) =PsiOptValue) 
C) =PsiOptIndex) 
D) =PsiCurrentOpt) 
A) =PsiOptNum) 
B) =PsiOptValue) 
C) =PsiOptIndex) 
D) =PsiCurrentOpt)

Question 2

Exhibit 4.1
The following questions are based on the problem below and accompanying Analytic Solver Platform sensitivity report.
Carlton construction is supplying building materials for a new mall construction project in Kansas.Their contract calls for a total of 250,000 tons of material to be delivered over a three-week period.Carlton's supply depot has access to three modes of transportation: a trucking fleet,railway delivery,and air cargo transport.Their contract calls for 120,000 tons delivered by the end of week one,80% of the total delivered by the end of week two,and the
entire amount delivered by the end of week three.Contracts in place with the transportation companies call for at least 45% of the total delivered be delivered by trucking,at least 40% of the total delivered be delivered by railway,and up to 15% of the total delivered be delivered by air cargo.Unfortunately,competing demands limit the availability of each mode of transportation each of the three weeks to the following levels all in thousands of tons):
 $\begin{array}{rrrr}
\text { Week } & \text { TruckingLimits } & \text { Railway Limits } & \text { Air Cargo Limits } \
\hline 1 & 45 & 60 & 15 \
2 & 50 & 55 & 10 \
3 & 55 & 45 & 5 \
\hline \text { Costs } \$ \text { per } 1000 \text { tons) } & \$ 200 & \$ 140 & \$ 400
\end{array}$
 The following is the LP model for this logistics problem.
Let S1U1P1XS1S1P0S1U1B1ij S1U1B0S1U1P1= amount shipped by mode i in week jS1S1P0
where i = 1Truck),2Rail),3Air)and j = 1,2,3
S1U1B1LetS1U1B0S1U1B1 S1U1B0WLS1U1B1ij S1U1B0= weekly limit of mode i in week j as provided in above table)
200XS1U1B111 S1U1B0+ XS1U1B112 S1U1B0+ XS1U1B113S1U1B0)+ 140XS1U1B121 S1U1B0+ XS1U1B122 S1U1B0+ XS1U1B123S1U1B0)+ 500XS1U1B131 S1U1B0+
MIN:
X + X )
Subject to:
32 33
S1U1P1XS1S1P0S1U1B1ij S1U1B0S1U1P1? WL S1S1P0S1U1B1ij S1U1B0S1U1P1for all i and jS1S1P0S1U1P1 S1S1P0Weekly limits by mode
XS1U1B111 S1U1B0+ XS1U1B112 S1U1B0+ XS1U1B113 S1U1B0+ XS1U1B121 S1U1B0+ XS1U1B122 S1U1B0+ XS1U1B123 S1U1B0+ XS1U1B131 S1U1B0+ XS1U1B132 S1U1B0+ XS1U1B133 S1U1B0? 250
Total at end of three weeks
S1U1P1XS1S1P0S1U1B111 S1U1B0S1U1P1+ XS1S1P0S1U1B121 S1U1B0S1U1P1+ XS1S1P0S1U1B131 S1U1B0S1U1P1+ XS1S1P0S1U1B112 S1U1B0S1U1P1+ XS1S1P0S1U1B122 S1U1B0S1U1P1+ XS1S1P0S1U1B132 S1U1B0S1U1P1? 200S1S1P0S1U1P1 S1S1P0Total at end of two weeks S1U1P1XS1S1P0S1U1B111 S1U1B0S1U1P1+ XS1S1P0S1U1B121 S1U1B0S1U1P1+ XS1S1P0S1U1B131 S1U1B0S1U1P1? 120S1S1P0S1U1P1 S1S1P0Total at end of first week
S1U1P1XS1S1P0S1U1B111 S1U1B0S1U1P1+ XS1S1P0S1U1B112 S1U1B0S1U1P1+ XS1S1P0S1U1B113 S1U1B0S1U1P1? 0.45*250S1S1P0S1U1P1 S1S1P0Truck mix requirement
S1U1P1XS1S1P0S1U1B121 S1U1B0S1U1P1+ XS1S1P0S1U1B122 S1U1B0S1U1P1+ XS1S1P0S1U1B123 S1U1B0S1U1P1? 0.40*250S1S1P0S1U1P1 S1S1P0Rail mix requirement
S1U1P1XS1S1P0S1U1B131 S1U1B0S1U1P1+ XS1S1P0S1U1B132 S1U1B0S1U1P1+ XS1S1P0S1U1B133 S1U1B0S1U1P1? 0.15*250S1S1P0S1U1P1 S1S1P0Air mix limit XS1U1B1ij S1U1B0? 0 for all i and j
 \(\begin{array}{rrrrrrr}
&&\text { Final } & \text { Reduced } & \text { Objective } & \text { Allowable } & \text { Allowable } \
&&\text { Value } & \text { Cost } & \text { Coefficient } & \text { Increase } & \text { Decrease }\
\text { Cell } & \text { Name } & & & & \
\hline \$ \mathrm{D} \$ 6 & \text { Week 1 by Truck } & 45 & 0 & 200 & 360 & 1 \mathrm{E}+30 \
\$ \mathrm{E} \$ 6 & \text { Week 1 by Rail } & 60 & 0 & 140 & 360 & 1 \mathrm{E}+30 \
\$ \mathrm{~F} \$ 6 & \text { Week 1 by Air } & 15 & 0 & 500 & 1 \mathrm{E}+30 & 360 \
\$ \mathrm{D} \$ 7 & \text { Week 2 by Truck } & 50 & 0 & 200 & 0 & 1 \mathrm{E}+30 \
\$ \mathrm{E} \$ 7 & \text { Week 2 by Rail } & 55 & 0 & 140 & 0 & 1 \mathrm{E}+30 \
\$ \mathrm{~F} \$ 7 & \text { Week 2 by Air } & 0 & 360 & 500 & 1 \mathrm{E}+30 & 360 \
\$ \mathrm{D} \$ 8 & \text { Week 3 by Truck } & 13 & 0 & 200 & 1 \mathrm{E}+30 & 0 \
\$ \mathrm{E} \$ 8 & \text { Week 3 by Rail } & 12 & 0 & 140 & 60 & 0 \
\$ F \$ 8 & \text { Week 3 by Air } & 0 & 360 & 500 & 1 \mathrm{E}+30 & 360
\end{array}\)
  
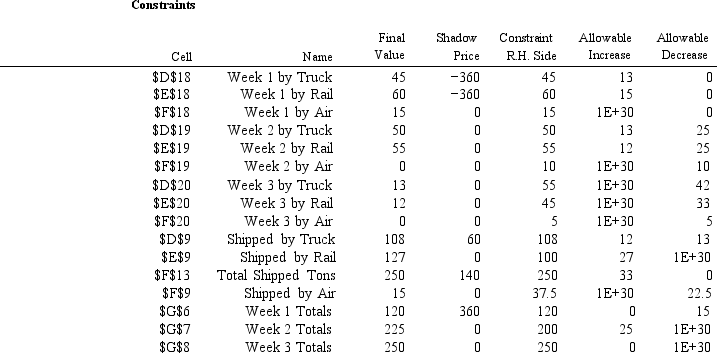-Refer to Exhibit 4.1.Of the three percentage of effort constraints,Shipped by Truck,Shipped by Rail,and Shipped by Air,which should be examined for potential cost reduction?

Accepted Answer

The percentage by Truck,Shippe

Question 3

The allowable increase for a changing cell decision variable)is

Accepted Answer

A) how many more units to produce to maximize profits. 
B) the amount by which the objective function coefficient can increase without changing the optimal solution. 
C) how much to charge to get the optimal solution. 
D) the amount by which constraint coefficient can increase without changing the optimal solution. 
A) how many more units to produce to maximize profits. 
B) the amount by which the objective function coefficient can increase without changing the optimal solution. 
C) how much to charge to get the optimal solution. 
D) the amount by which constraint coefficient can increase without changing the optimal solution.

Question 4

The Simplex method uses which of the following values to determine if the objective function value can be improved?

Accepted Answer

A) shadow price 
B) target value 
C) reduced cost 
D) basic cost 
A) shadow price 
B) target value 
C) reduced cost 
D) basic cost

Question 5

Exhibit 4.2
The following questions correspond to the problem below and associated Analytic Solver Platform sensitivity report.
Robert Hope received a welcome surprise in this management science class;the instructor has decided to let each person define the percentage contribution to their grade for each of the graded instruments used in the class.These instruments were: homework,an individual project,a mid-term exam,and a final exam.Robert's grades on these instruments were 75,94,85,and 92,respectively.However,the instructor complicated Robert's task somewhat by adding the following stipulations:
· homework can account for up to 25% of the grade,but must be at least 5% of the grade;
· the project can account for up to 25% of the grade,but must be at least 5% of the grade;
· the mid-term and final must each account for between 10% and 40% of the grade but cannot account for more than 70% of the grade when the percentages are combined;and
· the project and final exam grades may not collectively constitute more than 50% of the grade.The following LP model allows Robert to maximize his numerical grade.
Let S1U1P1WS1S1P0S1U1B11 S1U1B0S1U1P1= weight assigned to homework S1S1P0WS1U1B12 S1U1B0= weight assigned to the project WS1U1B13 S1U1B0= weight assigned to the mid-term WS1U1B14 S1U1B0= weight assigned to the final
MAX: S1U1P175WS1S1P0S1U1B11 S1U1B0S1U1P1+ 94WS1S1P0S1U1B12 S1U1B0S1U1P1+ 85WS1S1P0S1U1B13 S1U1B0S1U1P1+ 92WS1S1P0S1U1B14S1U1B0
Subject to: S1U1P1WS1S1P0S1U1B11 S1U1B0S1U1P1+ WS1S1P0S1U1B12 S1U1B0S1U1P1+ WS1S1P0S1U1B13 S1U1B0S1U1P1+ WS1S1P0S1U1B14 S1U1B0S1U1P1= 1S1S1P0
WS1U1B13 S1U1B0+ WS1U1B14 S1U1B0≤ 0.70 WS1U1B13 S1U1B0+ WS1U1B14 S1U1B0≥ 0.50 0.05 ≤ WS1U1B11 S1U1B0≤ 0.25
0.05 ≤ WS1U1B12 S1U1B0≤ 0.25
0.10 ≤ WS1U1B13 S1U1B0≤ 0.40
0.10 ≤ WS1U1B14 S1U1B0≤ 0.40
  
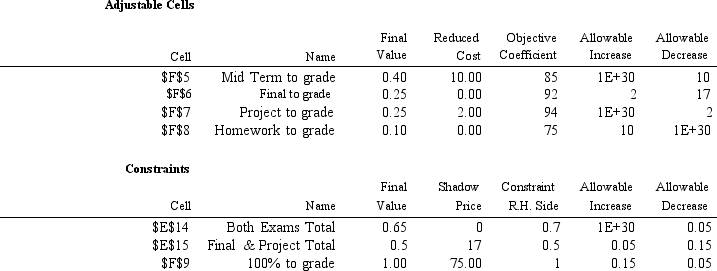-Refer to Exhibit 4.2.Constraint cell F9 corresponds to the constraint,W1 + W2 + W3 + W4 = 1,and has a shadow
price of 75.Armed with this information,what can Robert request of his instructor regarding this constraint?

Accepted Answer

Nothing.The constraint has the

Question 6

Analytic Solver Platform provides sensitivity analysis information on all of the following except the

Accepted Answer

A) range of values for objective function coefficients which do not change optimal solution. 
B) impact on optimal objective function value of changes in constrained resources. 
C) impact on optimal objective function value of changes in value of decision variables. 
D) impact on right hand sides of changes in constraint coefficients. 
A) range of values for objective function coefficients which do not change optimal solution. 
B) impact on optimal objective function value of changes in constrained resources. 
C) impact on optimal objective function value of changes in value of decision variables. 
D) impact on right hand sides of changes in constraint coefficients.

Question 7

A formulation has 20 variables and 8 constraints not counting non-negativity).How many variables are nonbasic?

Accepted Answer

A) 8 
B) 12 
C) 20 
D) 28 
A) 8 
B) 12 
C) 20 
D) 28

Question 8

When the allowable increase or allowable decrease for the objective function coefficient of one or more variables is zero it indicates in the absence of degeneracy)that

Accepted Answer

A) the problem is infeasible. 
B) alternate optimal solutions exist. 
C) there is only one optimal solution. 
D) no optimal solution can be found. 
A) the problem is infeasible. 
B) alternate optimal solutions exist. 
C) there is only one optimal solution. 
D) no optimal solution can be found.

Question 9

Benefits of sensitivity analysis include all the following except:

Accepted Answer

A) provides a better picture of how solutions change as model factors change. 
B) fosters managerial acceptance of the optimal solution. 
C) overcomes management skepticism of optimal solutions. 
D) answers potential managerial questions regarding the solution to an LP problem. 
A) provides a better picture of how solutions change as model factors change. 
B) fosters managerial acceptance of the optimal solution. 
C) overcomes management skepticism of optimal solutions. 
D) answers potential managerial questions regarding the solution to an LP problem.

Question 10

What is the value of the objective function if X1 is set to 0 in the following Limits Report?
$\begin{array}{rrr}
\text { Cell } & \begin{array}{c}
\text { Target } \
\text { Name }
\end{array} & \text { Value } \
\hline \$ E \$ 5 & \text { Unit profit: Total Profit: } & 3200
\end{array}$

Adjustable Lower Target Upper Target
Cell Name Value Limit Result Limit Result
$B$4 Number to make: X1 80 0 800 79.99999999 3200
$C$4 Number to make: X2 20 0 2400 20 3200

Accepted Answer

A) 80 
B) 800 
C) 2400 
D) 3200 
A) 80 
B) 800 
C) 2400 
D) 3200

Question 11

The coefficients in an LP model cj,aij,bj)represent

Accepted Answer

A) random variables. 
B) numeric constants. 
C) random constants. 
D) numeric variables. 
A) random variables. 
B) numeric constants. 
C) random constants. 
D) numeric variables.

Question 12

Jones Furniture Company produces beds and desks for college students.The production process requires carpentry and varnishing.Each bed requires 6 hours of carpentry and 4 hour of varnishing.Each desk requires 4 hours of carpentry and 8 hours of varnishing.There are 36 hours of carpentry time and 40 hours of varnishing time available.Beds generate $30 of profit and desks generate $40 of profit.Demand for desks is limited so at most 8 will be produced.
How much can the price of Desks drop before it is no longer profitable to produce them? Base your response on the following Analytic Solver Platform sensitivity output.
Let X1 = Number of Beds to produce X2 = Number of Desks to produce
The LP model for the problem is
MAX: 30 X1 + 40 X2
Subject to: 6 X1 + 4 X2 ? 36 carpentry)
4 X1 + 8 X2 ? 40 varnishing)X2 ? 8 demand for X2)
X1,X2 ? 0
 $\text { Changing Calls }$
$\begin{array}{rrrrrrr}
\text { Cell } & \text { Name } & \begin{array}{r}
\text { Final } \
\text { Value }
\end{array} & \begin{array}{r}
\text { Reduced } \
\text { Cost }
\end{array} & \begin{array}{r}
\text { Objective } \
\text { Coefficient }
\end{array} & \begin{array}{r}
\text { Allowable } \
\text { Increase }
\end{array} & \begin{array}{r}
\text { Allowable } \
\text { Decrease }
\end{array} \
\hline \$ B \$ 4 & \text { Number to make: Beds } & 4 & 0 & 30 & 30 & 10 \
\$ C \$ 4 & \text { Number to make: Desks } & 3 & 0 & 40 & 20 & 20
\end{array}$

$\text { Coustraints }$

$\begin{array}{rrrrrrr}
\text { Cell } & \text { Name } & \begin{array}{r}
\text { Final } \
\text { Value }
\end{array} & \begin{array}{r}
\text { Shadow } \
\text { Price }
\end{array} & \begin{array}{r}
\text { Constraint } \
\text { R.H. Side }
\end{array} & \begin{array}{r}
\text { Allowable } \
\text { Increase }
\end{array} & \begin{array}{r}
\text { Allowable } \
\text { Decrease }
\end{array} \
\hline \$ \mathrm{D} \$ 8 & \text { Carpentry Used } & 36 & 2.5 & 36 & 24 & 16 \
\$ \mathrm{D} \$ 9 & \text { Varnishing Used } & 40 & 3.75 & 40 & 26.67 & 16 \
\$ \mathrm{D} \$ 10 & \text { Desk demand Used } & 3 & 0 & 8 & 1 \mathrm{~E}+30 & 5
\end{array}$

Accepted Answer

The allowa

Question 13

The simplex method of linear programming LP):

Accepted Answer

A) considers only the extreme points of the feasible region to achieve efficiency in solving LP problems 
B) explicitly enumerates all corner points of the feasible region and selects the best objective function value 
C) evaluates all constraints for feasibility 
D) is not used in the Analytic Solver Platform software 
A) considers only the extreme points of the feasible region to achieve efficiency in solving LP problems 
B) explicitly enumerates all corner points of the feasible region and selects the best objective function value 
C) evaluates all constraints for feasibility 
D) is not used in the Analytic Solver Platform software

Question 14

Jones Furniture Company produces beds and desks for college students.The production process requires carpentry and varnishing.Each bed requires 6 hours of carpentry and 4 hour of varnishing.Each desk requires 4 hours of carpentry and 8 hours of varnishing.There are 36 hours of carpentry time and 40 hours of varnishing time available.Beds generate $30 of profit and desks generate $40 of profit.Demand for desks is limited so at most 8 will be produced.
Suppose the company can purchase more varnishing time for $3.00,should it be purchased and how much can be bought before the value of the additional time is uncertain? Base your response on the following Analytic Solver Platform sensitivity output.
Let X1 = Number of Beds to produce X2 = Number of Desks to produce
The LP model for the problem is
MAX: 30 X1 + 40 X2
Subject to: 6 X1 + 4 X2 ? 36 carpentry)
4 X1 + 8 X2 ? 40 varnishing)X2 ? 8 demand for X2)
X1,X2 ? 0
 $\text { Changing Calls }$
$\begin{array}{rrrrrrr}
\text { Cell } & \text { Name } & \begin{array}{r}
\text { Final } \
\text { Value }
\end{array} & \begin{array}{r}
\text { Reduced } \
\text { Cost }
\end{array} & \begin{array}{r}
\text { Objective } \
\text { Coefficient }
\end{array} & \begin{array}{r}
\text { Allowable } \
\text { Increase }
\end{array} & \begin{array}{r}
\text { Allowable } \
\text { Decrease }
\end{array} \
\hline \$ B \$ 4 & \text { Number to make: Beds } & 4 & 0 & 30 & 30 & 10 \
\$ C \$ 4 & \text { Number to make: Desks } & 3 & 0 & 40 & 20 & 20
\end{array}$

$\text { Coustraints }$

$\begin{array}{rrrrrrr}
\text { Cell } & \text { Name } & \begin{array}{r}
\text { Final } \
\text { Value }
\end{array} & \begin{array}{r}
\text { Shadow } \
\text { Price }
\end{array} & \begin{array}{r}
\text { Constraint } \
\text { R.H. Side }
\end{array} & \begin{array}{r}
\text { Allowable } \
\text { Increase }
\end{array} & \begin{array}{r}
\text { Allowable } \
\text { Decrease }
\end{array} \
\hline \$ \mathrm{D} \$ 8 & \text { Carpentry Used } & 36 & 2.5 & 36 & 24 & 16 \
\$ \mathrm{D} \$ 9 & \text { Varnishing Used } & 40 & 3.75 & 40 & 26.67 & 16 \
\$ \mathrm{D} \$ 10 & \text { Desk demand Used } & 3 & 0 & 8 & 1 \mathrm{~E}+30 & 5
\end{array}$

Accepted Answer

Yes,because the cost of $3.00

Question 15

A change in the right hand side of a constraint changes

Accepted Answer

A) the slope of the objective function 
B) objective function coefficients 
C) other right hand sides 
D) the feasible region 
A) the slope of the objective function 
B) objective function coefficients 
C) other right hand sides 
D) the feasible region

Question 16

Analytic Solver Platform provides all of the following reports except

Accepted Answer

A) Answer 
B) Sensitivity 
C) Cost performance 
D) Limits 
A) Answer 
B) Sensitivity 
C) Cost performance 
D) Limits

Question 17

What is the value of the slack variable in the following constraint when X1 and X2 are nonbasic and only non- negativity is used as simple bounds?
X1 + X2 + S1 = 100

Accepted Answer

A) 0 
B) 50 
C) 100 
D) can't be determined from the given information 
A) 0 
B) 50 
C) 100 
D) can't be determined from the given information

Question 18

The allowable decrease for a changing cell decision variable)is

Accepted Answer

A) the amount by which the constraint coefficient can decrease without changing final optimal solution. 
B) an indication of how many more units to produce to maximize profits. 
C) the amount by which objective function coefficient can decrease without changing the final optimal solution. 
D) an indication of how much to charge to get the optimal solution. 
A) the amount by which the constraint coefficient can decrease without changing final optimal solution. 
B) an indication of how many more units to produce to maximize profits. 
C) the amount by which objective function coefficient can decrease without changing the final optimal solution. 
D) an indication of how much to charge to get the optimal solution.

Question 19

What needs to be done to the two constraints in order to convert the problem to a standard form?
MAX: 8 X1 + 4 X2
Subject to: 5 X1 + 5 X2 ≤ 20
6 X1 + 2 X2 ≤ 18 X1,X2 ≥ 0

Accepted Answer

A) a slack variable needs to be added to each constraint to convert them to equalities. 
B) nothing. 
C) they need to be combined to a single constraint. 
D) they need to be subtracted side-by-side 
A) a slack variable needs to be added to each constraint to convert them to equalities. 
B) nothing. 
C) they need to be combined to a single constraint. 
D) they need to be subtracted side-by-side

Question 20

Solve this problem graphically.What is the optimal solution and what constraints are binding at the optimal solution?
MAX: 8 X1 + 4 X2
Subject to: 5 X1 + 5 X2 ≤ 20
6 X1 + 2 X2 ≤ 18 X1,X2 ≥ 0

Accepted Answer

Obj = 26 X₁= 2.5 X₂= 1

When automatically running multiple optimizations in Analytic Solver Platform,what spreadsheet function indicates which optimization is being run?

The allowable increase for a changing cell decision variable)is

The Simplex method uses which of the following values to determine if the objective function value can be improved?

Analytic Solver Platform provides sensitivity analysis information on all of the following except the

A formulation has 20 variables and 8 constraints not counting non-negativity).How many variables are nonbasic?

When the allowable increase or allowable decrease for the objective function coefficient of one or more variables is zero it indicates in the absence of degeneracy)that

Benefits of sensitivity analysis include all the following except:

The coefficients in an LP model c_j,a_ij,b_j)represent

The simplex method of linear programming LP):

A change in the right hand side of a constraint changes

Analytic Solver Platform provides all of the following reports except

What is the value of the slack variable in the following constraint when X₁and X₂are nonbasic and only non- negativity is used as simple bounds? X₁+ X₂+ S₁= 100

The allowable decrease for a changing cell decision variable)is

What needs to be done to the two constraints in order to convert the problem to a standard form? MAX: ^{8 X}₁^{+ 4 X}₂ Subject to: ^{5 X}₁^{+ 5 X}₂^{≤ 20} 6 X₁+ 2 X₂≤ 18 X₁,X₂≥ 0

Solve this problem graphically.What is the optimal solution and what constraints are binding at the optimal solution? MAX: ^{8 X}₁^{+ 4 X}₂ Subject to: ^{5 X}₁^{+ 5 X}₂^{≤ 20} 6 X₁+ 2 X₂≤ 18 X₁,X₂≥ 0

Introduction to Modeling and Decision Analysis

Introduction to Optimization and Linear Programming

Modeling and Solving Lp Problems in a Spreadsheet

Network Modeling

Integer Linear Programming

Goal Programming and Multiple Objective Optimization

Nonlinear Programming and Evolutionary Optimization

Regression Analysis

Data Mining

Time Series Forecasting

Introduction to Simulation Using Analytic Solver Platform

Queuing Theory

Decision Analysis

Project Management Online

Filters

Exam 4: Sensitivity Analysis and the Simplex Method

When automatically running multiple optimizations in Analytic Solver Platform,what spreadsheet function indicates which optimization is being run?

The allowable increase for a changing cell decision variable)is

The Simplex method uses which of the following values to determine if the objective function value can be improved?

Analytic Solver Platform provides sensitivity analysis information on all of the following except the

A formulation has 20 variables and 8 constraints not counting non-negativity).How many variables are nonbasic?

When the allowable increase or allowable decrease for the objective function coefficient of one or more variables is zero it indicates in the absence of degeneracy)that

Benefits of sensitivity analysis include all the following except:

The coefficients in an LP model cj,aij,bj)represent

The simplex method of linear programming LP):

A change in the right hand side of a constraint changes

Analytic Solver Platform provides all of the following reports except

What is the value of the slack variable in the following constraint when X1 and X2 are nonbasic and only non- negativity is used as simple bounds? X1 + X2 + S1 = 100

The allowable decrease for a changing cell decision variable)is

What needs to be done to the two constraints in order to convert the problem to a standard form? MAX: 8 X1 + 4 X2 Subject to: 5 X1 + 5 X2 ≤ 20 6 X1 + 2 X2 ≤ 18 X1,X2 ≥ 0

Solve this problem graphically.What is the optimal solution and what constraints are binding at the optimal solution? MAX: 8 X1 + 4 X2 Subject to: 5 X1 + 5 X2 ≤ 20 6 X1 + 2 X2 ≤ 18 X1,X2 ≥ 0

Introduction to Modeling and Decision Analysis

Introduction to Optimization and Linear Programming

Modeling and Solving Lp Problems in a Spreadsheet

Network Modeling

Integer Linear Programming

Goal Programming and Multiple Objective Optimization

Nonlinear Programming and Evolutionary Optimization

Regression Analysis

Data Mining

Time Series Forecasting

Introduction to Simulation Using Analytic Solver Platform

Queuing Theory

Decision Analysis

Project Management Online

Filters

The coefficients in an LP model c_j,a_ij,b_j)represent

What is the value of the slack variable in the following constraint when X₁and X₂are nonbasic and only non- negativity is used as simple bounds? X₁+ X₂+ S₁= 100

What needs to be done to the two constraints in order to convert the problem to a standard form? MAX: ^{8 X}₁^{+ 4 X}₂ Subject to: ^{5 X}₁^{+ 5 X}₂^{≤ 20} 6 X₁+ 2 X₂≤ 18 X₁,X₂≥ 0

Solve this problem graphically.What is the optimal solution and what constraints are binding at the optimal solution? MAX: ^{8 X}₁^{+ 4 X}₂ Subject to: ^{5 X}₁^{+ 5 X}₂^{≤ 20} 6 X₁+ 2 X₂≤ 18 X₁,X₂≥ 0