Chat with AIExam 4: Integrals
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
for 
and some number
a.
Let ![Let . a.Use Part 1 of the Fundamental Theorem of Calculus to find . b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for F(x). c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1 If f is continuous on [a, b], then the function F defined by is differentiable on (a, b), and The Fundamental Theorem of Calculus, Part 2 If f is continuous on [a, b], then where F is any antiderivative of f, that is, .](https://storage.examlex.com/TB5971/11eaa3e5_55a5_f8b3_9f8f_d3756c7e286e_TB5971_11.jpg)
.
a.Use Part 1 of the Fundamental Theorem of Calculus to find ![Let . a.Use Part 1 of the Fundamental Theorem of Calculus to find . b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for F(x). c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1 If f is continuous on [a, b], then the function F defined by is differentiable on (a, b), and The Fundamental Theorem of Calculus, Part 2 If f is continuous on [a, b], then where F is any antiderivative of f, that is, .](https://storage.examlex.com/TB5971/11eaa3e5_55a6_1fc4_9f8f_139ea51780a1_TB5971_11.jpg)
.
b.Use Part 2 of the Fundamental Theorem of Calculus to integrate ![Let . a.Use Part 1 of the Fundamental Theorem of Calculus to find . b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for F(x). c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1 If f is continuous on [a, b], then the function F defined by is differentiable on (a, b), and The Fundamental Theorem of Calculus, Part 2 If f is continuous on [a, b], then where F is any antiderivative of f, that is, .](https://storage.examlex.com/TB5971/11eaa3e5_55a6_1fc5_9f8f_035219f062fe_TB5971_11.jpg)
to obtain an alternative expression for F(x).
c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1
If f is continuous on [a, b], then the function F defined by ![Let . a.Use Part 1 of the Fundamental Theorem of Calculus to find . b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for F(x). c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1 If f is continuous on [a, b], then the function F defined by is differentiable on (a, b), and The Fundamental Theorem of Calculus, Part 2 If f is continuous on [a, b], then where F is any antiderivative of f, that is, .](https://storage.examlex.com/TB5971/11eaa3e5_55a6_46d6_9f8f_4f4da712b2a5_TB5971_11.jpg)
is differentiable on (a, b), and ![Let . a.Use Part 1 of the Fundamental Theorem of Calculus to find . b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for F(x). c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1 If f is continuous on [a, b], then the function F defined by is differentiable on (a, b), and The Fundamental Theorem of Calculus, Part 2 If f is continuous on [a, b], then where F is any antiderivative of f, that is, .](https://storage.examlex.com/TB5971/11eaa3e5_55a6_46d7_9f8f_c3bc40309522_TB5971_11.jpg)
The Fundamental Theorem of Calculus, Part 2
If f is continuous on [a, b], then ![Let . a.Use Part 1 of the Fundamental Theorem of Calculus to find . b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for F(x). c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1 If f is continuous on [a, b], then the function F defined by is differentiable on (a, b), and The Fundamental Theorem of Calculus, Part 2 If f is continuous on [a, b], then where F is any antiderivative of f, that is, .](https://storage.examlex.com/TB5971/11eaa3e5_55a6_46d8_9f8f_91f5f7a42169_TB5971_11.jpg)
where F is any antiderivative of f, that is, ![Let . a.Use Part 1 of the Fundamental Theorem of Calculus to find . b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for F(x). c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1 If f is continuous on [a, b], then the function F defined by is differentiable on (a, b), and The Fundamental Theorem of Calculus, Part 2 If f is continuous on [a, b], then where F is any antiderivative of f, that is, .](https://storage.examlex.com/TB5971/11eaa3e5_55a6_6de9_9f8f_cf10a69dd2cf_TB5971_11.jpg)
.
.
a.Use Part 1 of the Fundamental Theorem of Calculus to find .
b.Use Part 2 of the Fundamental Theorem of Calculus to integrate to obtain an alternative expression for F(x).
c.Differentiate the expression for F(x) found in part (b).The Fundamental Theorem of Calculus, Part 1
If f is continuous on [a, b], then the function F defined by
is differentiable on (a, b), and
The Fundamental Theorem of Calculus, Part 2
If f is continuous on [a, b], then
where F is any antiderivative of f, that is, . (Essay)
4.8/5 
(39)
(39) 
, 
The table gives the values of a function obtained from an experiment. Use the values to estimate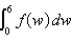 
using three equal subintervals with left endpoints.
w
0
1
2
3
4
5
6
f (w)
9.7
9.1
7.7
6.1
4.2
-6.6
-10.3
using three equal subintervals with left endpoints.
w
0
1
2
3
4
5
6
f (w)
9.7
9.1
7.7
6.1
4.2
-6.6
-10.3 (Short Answer)
4.8/5 (44)
(44) 
.
Use the Midpoint Rule with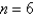 
to approximate the integral. Round the answer to 3 decimal places. 
to approximate the integral. Round the answer to 3 decimal places.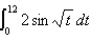 (Essay)
4.7/5 (39)
(39) The acceleration function (in m / s2) and the initial velocity are given for a particle moving along a line. Find the velocity at time t and the distance traveled during the given time interval.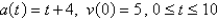 
(Multiple Choice)
4.8/5 (34)
(34) 
The given expression is the limit of a Riemann sum of a function f on [a, b]. Write this expression as a definite integral on [a, b]. ![The given expression is the limit of a Riemann sum of a function f on [a, b]. Write this expression as a definite integral on [a, b].](https://storage.examlex.com/TB5971/11eaa3e5_55a7_f49f_9f8f_57d42db5275a_TB5971_11.jpg)
(Multiple Choice)
4.8/5 (39)
(39) The velocity function (in meters per second) is given for a particle moving along a line. Find the distance traveled by the particle during the given time interval.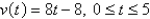 
(Multiple Choice)
4.9/5 (25)
(25) 
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)