Exam 12: Vectors and the Geometry of Space
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Find the midpoint of the line segment joining the given points. (-5, 0, 2) and (-3, -2, 4)
(Multiple Choice)
4.8/5  (44)
(44)
Suppose you start at the origin, move along the x-axis a distance of units in the positive direction, and then move downward a distance of units. What are the coordinates of your position?
(Multiple Choice)
4.8/5  (31)
(31)
Write an inequality to describe the half-space consisting of all points to the left of a plane parallel to the xz-plane and units to the right of it.
(Short Answer)
4.8/5  (38)
(38)
Find the length of the median of side AB of the triangle with vertices
(Short Answer)
4.9/5  (28)
(28)
Find the standard equation of the sphere with center C and radius r. C (3, -5, 3); r = 7
(Multiple Choice)
4.9/5  (37)
(37)
Find an equation of the plane that passes through the line of intersection of the planes and is perpendicular to the plane
(Short Answer)
4.9/5  (35)
(35)
Find an equation of the sphere that passes through the point and has center .
(Short Answer)
4.8/5  (37)
(37)
Find an equation of the plane that passes through the point and contains the line
(Short Answer)
4.8/5  (36)
(36)
Determine whether the given points are collinear. A (-3, -2, -3), B (-9, -5, 0), and C (-1, -1, -4)
(Multiple Choice)
4.9/5  (36)
(36)
Write inequalities to describe the solid upper hemisphere of the sphere of radius centered at the origin.
(Short Answer)
5.0/5  (33)
(33)
Two forces with magnitudes 8 lb and 12 lb act on an object at a point P as shown in the figure. Find the magnitude of the resultant force F acting at P. Round the result to the nearest tenth. 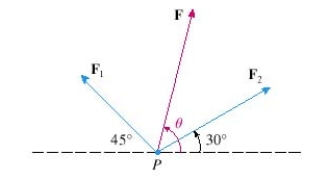
(Multiple Choice)
4.9/5  (30)
(30)
Find a nonzero vector orthogonal to the plane through the points P, Q, and R.
(Multiple Choice)
4.8/5  (28)
(28)
Write an inequality to describe the region consisting of all points between (but not on) the
spheres of radius and centered at the origin.
(Short Answer)
4.8/5  (40)
(40)
Sketch the plane in a three-dimensional space represented by the equation. z = 2
(Multiple Choice)
4.9/5  (37)
(37)
Find an equation of the plane with x-intercept , y-intercept and z-intercept .
(Multiple Choice)
4.9/5  (36)
(36)
Find parametric equations for the line through and parallel to the vector
(Short Answer)
4.9/5  (42)
(42)
Let and let u be a vector with length that starts at the origin and rotates in the xy - plane. Find the maximum value of the length of the vector .
(Multiple Choice)
4.8/5  (33)
(33)
Find the work done by a force that moves an object from the point to the point along a straight line. The distance is measured in meters and the force in newtons.
(Multiple Choice)
4.9/5  (40)
(40)
Showing 21 - 40 of 60
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)