Exam 5: Applications of Integration
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Estimate the area from 0 to 5 under the graph of using five approximating rectangles and right endpoints.
(Multiple Choice)
4.9/5  (42)
(42)
Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function.
(Short Answer)
4.7/5  (38)
(38)
If , find the Riemann sum with n = 5 correct to 3 decimal places, taking the sample points to be midpoints.
(Short Answer)
4.9/5  (40)
(40)
The area of the region that lies to the right of the y-axis and to the left of the parabola (the shaded region in the figure) is given by the integral . Find the area.. 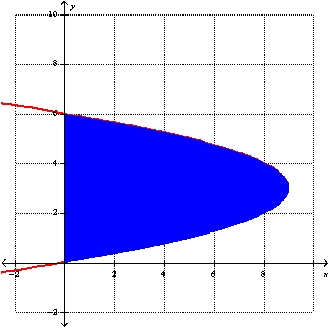
(Multiple Choice)
4.9/5  (36)
(36)
The velocity graph of a braking car is shown. Use it to estimate to the nearest foot the distance traveled by the car while the brakes are applied.Use a left sum with n = 7. 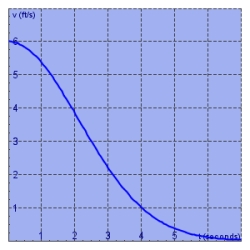
(Short Answer)
4.8/5  (32)
(32)
The velocity graph of a car accelerating from rest to a speed of 7 km/h over a period of 10 seconds is shown. Estimate to the nearest integer the distance traveled during this period. Use a right sum with . 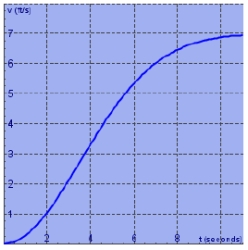
(Short Answer)
4.8/5  (39)
(39)
The velocity of a car was read from its speedometer at ten-second intervals and recorded in the table. Use the Midpoint Rule to estimate the distance traveled by the car. 0 0
60 54 10 70 20 80 30 90 40 100 50
(Multiple Choice)
4.7/5  (35)
(35)
Use the definition of area to find the area of the region under the graph of f on [a, b] using the indicated choice of ck. = , [0, 2], ck is the left endpoint
(Short Answer)
4.9/5  (39)
(39)
Approximate the area under the curve from 1 to 2 using ten approximating rectangles of equal widths and right endpoints. Round the answer to the nearest hundredth.
(Short Answer)
4.8/5  (30)
(30)
Use the definition of area to find the area of the region under the graph of f on [a, b] using the indicated choice of ck. = + 6x + 1, [ , 1], ck is the right endpoint
(Short Answer)
4.9/5  (33)
(33)
Express the integral as a limit of sums. Then evaluate the limit.
(Short Answer)
4.9/5  (47)
(47)
Showing 41 - 60 of 70
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)