Exam 9: Random Variables and Probability Distributions
Exam 2: Data28 Questions
Exam 3: Surveys and Sampling28 Questions
Exam 4: Displaying and Describing Categorical Data32 Questions
Exam 5: Displaying and Describing Quantitative Data32 Questions
Exam 6: Scatterplots, Association, and Correlation32 Questions
Exam 7: Introduction to Linear Regression32 Questions
Exam 8: Randomness and Probability32 Questions
Exam 9: Random Variables and Probability Distributions28 Questions
Exam 10: Sampling Distributions28 Questions
Exam 11: Confidence Intervals for Proportions32 Questions
Exam 12: Testing Hypotheses About Proportions36 Questions
Exam 13: Confidence Intervals and Hypothesis Tests for Means36 Questions
Exam 14: Comparing Two Means32 Questions
Exam 15: Design of Experiments and Analysis of Variance Anova24 Questions
Exam 16: Inference for Counts: Chi-Square Tests26 Questions
Exam 17: Nonparametric Methods23 Questions
Exam 18: Inference for Regression32 Questions
Exam 19: Understanding Regression Residuals28 Questions
Exam 20: Multiple Regression22 Questions
Exam 21: Building Multiple Regression Models22 Questions
Exam 22: Time Series Analysis28 Questions
Exam 23: Decision Making and Risk32 Questions
Exam 24: Quality Control28 Questions
Exam 25: Exploring and Collecting Data28 Questions
Exam 26: Understanding Probability Distributions and Statistical Inference70 Questions
Exam 27: Exploring Relationships Among Variables40 Questions
Exam 28: Using Statistics for Decision Making26 Questions
Select questions type
A company's manufacturing process uses 500 litres of water at a time. A "scrubbing" machine then removes most of a chemical pollutant before pumping the water into a nearby lake. To meet federal regulations the treated water must not contain more than 80 parts per million (ppm) of the chemical. Because there is a fine charged if regulations are not met, the company sets the machine to attain an average of 75 ppm in the treated water. The machine's output can be described by a Normal model with a standard deviation 4.2 ppm.
a. What percent of the batches of water discharged exceed the 80 ppm standard?
b. The company's lawyers insist that not more than 2% of the treated water should be over the limit. In order to achieve this, to what mean should the company set the scrubbing machine? Assume the standard deviation does not change.
Free
(Essay)
4.8/5  (40)
(40)
Correct Answer:
a. z = 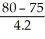 = 1.19
= 1.19
P(z ≥ 1.19) ≈ 0.117
b. z = 2.054 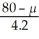 = 2.054
= 2.054
μ ≈ 71.373
Cars arrive randomly and independently at a drive through service centre at a rate of 10 per hour. What is the probability that 2 or 3 cars will arrive in a 15 minute period?
Free
(Multiple Choice)
4.9/5  (30)
(30)
Correct Answer:
A
Consider the following to answer the question(s) below:
An airline has found that its flights between Toronto and Vancouver can take anywhere from 4.5 - 7.5 hours, with any time between this range being equally likely.
-What is the probability that the flight will take more than 7 hours?
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
D
Consider the following to answer the question(s) below:
An airline has found that its flights between Toronto and Vancouver can take anywhere from 4.5 - 7.5 hours, with any time between this range being equally likely.
-What is the standard deviation?
(Multiple Choice)
4.8/5  (36)
(36)
The manager of a computer help desk operation in Moncton has collected enough data to conclude that the time per call is normally distributed with a mean equal to 8.21 minutes and a standard deviation of 2.14 minutes. The manager wants to set the time limit at a level such that it will sound on only 8 percent of all calls. The time limit should be
(Multiple Choice)
4.8/5  (39)
(39)
Consider the following to answer the question(s) below:
At a local manufacturing plant, employees must complete new machine set ups within 30 minutes. New machine set-up times can be described by a Normal model with a mean of 22 minutes and a standard deviation of four minutes.
-What percent of new machine set ups take more than 30 minutes?
(Multiple Choice)
4.8/5  (31)
(31)
Consider the following to answer the question(s) below:
The number of clients arriving at a bank machine is Poisson distributed with an average of 2 per minute. For a 5 minute period,
-What is the probability that no more than 2 customers will arrive in a 5 minute period?
(Multiple Choice)
4.8/5  (33)
(33)
Consider the following to answer the question(s) below:
At a local manufacturing plant, employees must complete new machine set ups within 30 minutes. New machine set-up times can be described by a Normal model with a mean of 22 minutes and a standard deviation of four minutes.
-The typical worker needs five minutes to adjust to their surroundings before beginning their duties. What percent of new machine set ups are completed within 25 minutes to allow for this?
(Multiple Choice)
5.0/5  (36)
(36)
Consider the following to answer the question(s) below:
A company's manufacturing process uses 500 litres of water at a time. A "scrubbing" machine then removes most of a chemical pollutant before pumping the water into a nearby lake. To meet federal regulations the treated water must not contain more than 80 parts per million (ppm) of the chemical. Because there is a fine charged if regulations are not met, the company sets the machine to attain an average of 75 ppm in the treated water. The machine's output can be described by a Normal model with a standard deviation 4.2 ppm.
-The company's lawyers insist that not more than 2% of the treated water should be over the limit. In order to achieve this, to what mean should the company set the scrubbing machine? Assume the standard deviation does not change.
(Multiple Choice)
4.8/5  (29)
(29)
The manager of a computer help desk operation in Moncton has collected enough data to conclude that the time per call is normally distributed with a mean equal to 8.21 minutes and a standard deviation of 2.14 minutes. Based on this, what is the probability that a call will last longer than 13 minutes?
(Multiple Choice)
4.8/5  (40)
(40)
The owner of a pet store is trying to decide whether to discontinue selling specialty clothes for pets. She suspects that only 4% of the customers buy specialty clothes for their pets and thinks that she might be able to replace the clothes with more profitable items. Before making a final decision, she decides to keep track of the total number of customers for a day and whether they purchase specialty clothes.
a. The owner had 275 customers that day. Assuming this was a typical day for her store, what would be the mean and standard deviation of the number of customers who buy specialty clothes for their pet each day?
b. Surprised by the high number of customers who purchased specialty pet clothing that day, the owner decided that her 4% estimate must have been too low. How many clothing sales would it have taken to convince you? Justify your answer.
(Essay)
4.8/5  (26)
(26)
Consider the following to answer the question(s) below:
A company believes that there will be a 50% chance of making a profit of $1,000, a 30% chance of making a profit of $1500 and a 20% chance of making a profit of $2,000.
-Find the standard deviation for the company's profit?
(Multiple Choice)
4.9/5  (30)
(30)
Consider the following to answer the question(s) below:
A courier service claims that no more than 5 % of all of its deliveries arrive late. Assuming deliveries are independent, a sample of 10 deliveries is randomly selected.
-What is the probability that exactly 2 of the sample deliveries arrives late?
(Multiple Choice)
4.8/5  (32)
(32)
Consider the following to answer the question(s) below:
A courier service claims that no more than 5 % of all of its deliveries arrive late. Assuming deliveries are independent, a sample of 10 deliveries is randomly selected.
-What is the probability that more than 2 of the sample deliveries arrive late?
(Multiple Choice)
4.8/5  (35)
(35)
It is assumed that the time between failures for an electronic component are exponentially distributed with a mean of 50 hours between consecutive failures. Based on this information, what is the probability that a randomly selected part will fail in less than 10 hours?
(Multiple Choice)
4.7/5  (35)
(35)
Cars arrive randomly and independently at a drive through service centre at a rate of 10 per hour. What is the probability that no cars will arrive in a 15 minute period?
(Multiple Choice)
4.8/5  (36)
(36)
The manager of a computer help desk operation in Moncton has collected enough data to conclude that the time per call is normally distributed with a mean equal to 8.21 minutes and a standard deviation of 2.14 minutes. What is the probability that three randomly monitored calls will each be completed in 4 minutes or less?
(Multiple Choice)
4.8/5  (36)
(36)
The number of calls received by a call centre follows a Poisson distribution with an average of 5 calls per minute. For a 1 minute period,
a. Find the expected value.
b. Find the probability of receiving no more than 2 calls.
(Essay)
4.8/5  (28)
(28)
Consider the following to answer the question(s) below:
A company's manufacturing process uses 500 litres of water at a time. A "scrubbing" machine then removes most of a chemical pollutant before pumping the water into a nearby lake. To meet federal regulations the treated water must not contain more than 80 parts per million (ppm) of the chemical. Because there is a fine charged if regulations are not met, the company sets the machine to attain an average of 75 ppm in the treated water. The machine's output can be described by a Normal model with a standard deviation 4.2 ppm.
-What percent of the batches of water discharged exceed the 80 ppm standard?
(Multiple Choice)
4.9/5  (27)
(27)
The number of plants that are found in a field averages 2 per square metre and follows a Poisson distribution. Based on this,
a. What is the expected value?
b. What is the probability that a 1-square metre section will contain less than 3 plants?.
(Essay)
4.9/5  (38)
(38)
Showing 1 - 20 of 28
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)