Exam 18: Fundamental Theorems of Vector Analysis
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
Use Stokes' Theorem to compute the line integral of 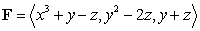 counterclockwise (as viewed from above) around the triangle with vertices
counterclockwise (as viewed from above) around the triangle with vertices 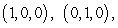 and
and 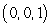 .
.
(Essay)
5.0/5  (43)
(43)
Calculate the circulation of the vector field 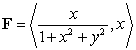 around the circle
around the circle 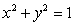 , traversed in a counterclockwise direction.
, traversed in a counterclockwise direction.
(Essay)
4.9/5  (39)
(39)
Evaluate 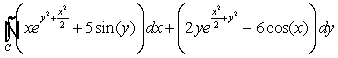 where
where 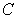 is the boundary of the unit square
is the boundary of the unit square 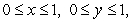 oriented clockwise.
oriented clockwise.
(Essay)
4.8/5  (38)
(38)
Evaluate 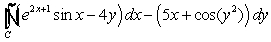 where
where 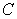 is the triangle with vertices
is the triangle with vertices 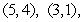 and
and 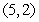 , traversed in a counterclockwise direction.
, traversed in a counterclockwise direction.
(Essay)
4.8/5  (42)
(42)
Evaluate 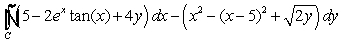 where
where 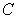 is the circle
is the circle 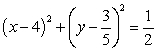 , traversed in a counterclockwise direction.
, traversed in a counterclockwise direction.
(Essay)
4.8/5  (38)
(38)
Use Stokes' Theorem to compute the line integral 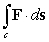 where
where 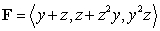 and c is the path made up of the sequence of three line segments:
0 to A, A to B, and B to C. (See the figure.)
and c is the path made up of the sequence of three line segments:
0 to A, A to B, and B to C. (See the figure.) 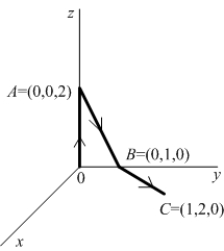
(Essay)
4.9/5  (43)
(43)
Evaluate 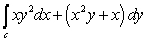 where c is the closed curve
where c is the closed curve 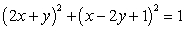 traversed in a counterclockwise direction.
traversed in a counterclockwise direction.
(Essay)
5.0/5  (30)
(30)
Let S be the upper half of the hemisphere 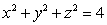 including the bottom
including the bottom 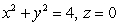 .
S is oriented with outward-pointing normal, and F is the vector field
.
S is oriented with outward-pointing normal, and F is the vector field 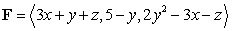 Compute
Compute 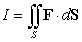 .
.
(Essay)
4.7/5  (44)
(44)
Compute 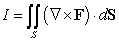 where
where 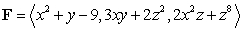 and S is the upper half of the sphere of radius 3, that is,
and S is the upper half of the sphere of radius 3, that is, 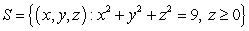 with upward-pointing normal.
with upward-pointing normal.
(Essay)
4.8/5  (37)
(37)
Evaluate 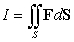 where
where 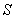 is the boundary of the region enclosed by the surfaces
is the boundary of the region enclosed by the surfaces 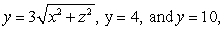 and
and 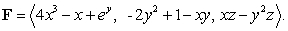
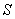 is oriented with inward-pointing normal.
is oriented with inward-pointing normal.
(Essay)
4.8/5  (30)
(30)
Let  be the vector field
be the vector field 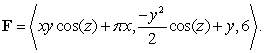 Compute the flux of
Compute the flux of 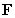 through the surface
through the surface 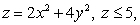 if the normal
if the normal 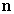 to the surface satisfies
to the surface satisfies 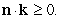
(Essay)
4.8/5  (40)
(40)
Let 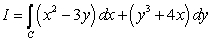 where C is the ellipse
where C is the ellipse 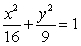 oriented counterclockwise. The value of I is which of the following?
oriented counterclockwise. The value of I is which of the following?
(Multiple Choice)
5.0/5  (42)
(42)
Use the Divergence Theorem to evaluate 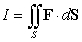 where
where 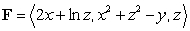 and S is the surface
and S is the surface 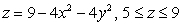 , oriented outward.
, oriented outward.
(Essay)
4.9/5  (38)
(38)
Compute 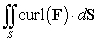 where
where 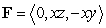 and S is the surface defined by
and S is the surface defined by 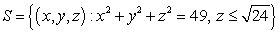 ,
oriented with outward pointing normal.
,
oriented with outward pointing normal.
(Essay)
4.8/5  (37)
(37)
Let 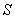 be the surface area of the box in the figure with dimensions
be the surface area of the box in the figure with dimensions 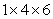 , and let W be the interior of the box.
, and let W be the interior of the box. 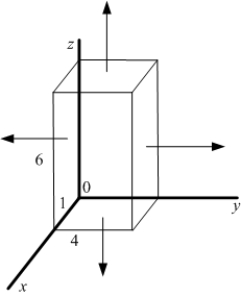 Let F be the vector field
Let F be the vector field 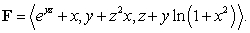 Which of the following integrals are equal?
A)
Which of the following integrals are equal?
A) 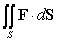 B)
B) 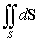 C)
C) 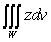 D)
D) 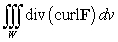 E)
E) 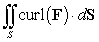
(Short Answer)
4.9/5  (32)
(32)
Compute the 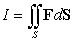 where
where 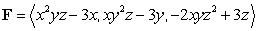 and
and 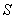 is the boundary of the tetrahedron with vertices
is the boundary of the tetrahedron with vertices 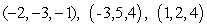 and
and 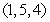 , oriented with outward-pointing normal.
, oriented with outward-pointing normal.
(Essay)
4.9/5  (45)
(45)
Evaluate 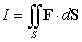 where
where 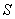 is the boundary of the upper hemisphere
is the boundary of the upper hemisphere 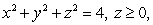 and
and 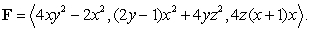 Assume
Assume 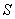 is oriented with outward-pointing normal.
is oriented with outward-pointing normal.
(Essay)
4.9/5  (31)
(31)
Evaluate 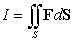 where
where 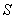 is the boundary of the region enclosed by the surfaces
is the boundary of the region enclosed by the surfaces 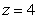 and
and 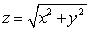 and
and 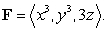
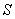 is oriented with outward-pointing normal.
is oriented with outward-pointing normal.
(Essay)
5.0/5  (35)
(35)
Compute the area of the shaded region whose boundary consists of the line segment 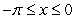 on the x axis and the curve
on the x axis and the curve 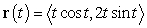 ,
, 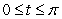 .
. 
(Essay)
4.8/5  (40)
(40)
Showing 21 - 40 of 91
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)