Exam 17: Line and Surface Integrals
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
Let 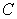 be the curve
be the curve 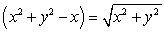 .
A) Parametrize
.
A) Parametrize 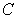 using polar coordinates.
B) Find the length of
using polar coordinates.
B) Find the length of 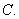
(Essay)
4.9/5  (37)
(37)
Compute the work performed in moving a particle along the path 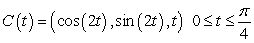 by the force
by the force 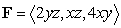 .
.
(Essay)
4.9/5  (39)
(39)
Compute the surface integral 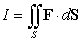 where
where 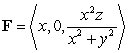 and S is the part of the sphere
and S is the part of the sphere 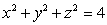 between the planes
between the planes 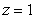 and
and 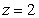 oriented outward.
oriented outward.
(Essay)
4.8/5  (39)
(39)
Let 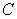 denote the closed curve of intersection of the hemisphere
denote the closed curve of intersection of the hemisphere 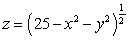 and the cylinder
and the cylinder 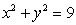 oriented counterclockwise.
Compute
oriented counterclockwise.
Compute 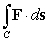 where
where 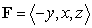 .
.
(Essay)
4.7/5  (40)
(40)
Compute 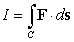 , where
, where 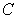 is the part of the ellipse
is the part of the ellipse 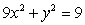 joining the point
joining the point 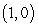 to the point
to the point 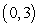 and
and 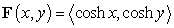 .
.
(Essay)
4.7/5  (39)
(39)
Compute the flux of the vector field 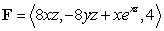 through the surface of the portion of the paraboloid
through the surface of the portion of the paraboloid 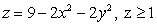 with outward-pointing normal.
with outward-pointing normal.
(Essay)
4.9/5  (41)
(41)
Compute 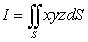 where S is the part of the plane
where S is the part of the plane 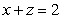 in the first octant bounded by the planes
in the first octant bounded by the planes 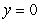 and
and 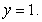
(Essay)
4.9/5  (33)
(33)
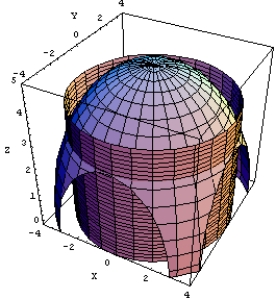
Let S be the surface above the 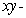 plane bounded by the sphere
plane bounded by the sphere 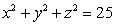 from above and by the cylinder
from above and by the cylinder 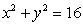 at the sides.
Compute
at the sides.
Compute 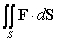 if
if 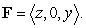
(Short Answer)
4.8/5  (34)
(34)
Let C be the curve 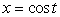 ,
, 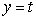 ,
, 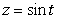 ,
, 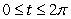 , and let
, and let 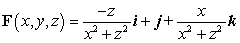 .
The value of
.
The value of 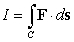 is which of the following?
is which of the following?
(Multiple Choice)
4.9/5  (28)
(28)
The mass of the part of the cone 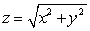 with
with 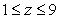 and density
and density 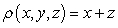 is which of the following?
is which of the following?
(Multiple Choice)
4.9/5  (44)
(44)
Showing 21 - 40 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)