Exam 14: Calculus of Vector-Valued Functions
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
Particle 1 follows the path parametrized by 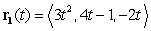 , while Particle 2 follows the path parametrized by
, while Particle 2 follows the path parametrized by 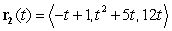 . At what time
. At what time 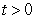 does the speed of Particle 1 match the speed of Particle 2?
does the speed of Particle 1 match the speed of Particle 2?
(Essay)
4.7/5  (42)
(42)
Find a parameterization for the line of intersection of the planes 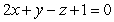 and
and 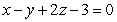 .
.
(Essay)
4.9/5  (36)
(36)
A satellite traverses a circular orbit about the Earth at a speed of 1100 m/s. How far removed from the Earth's surface is the satellite's orbit? Assume the Earth has a radius of 6500 km and mass of 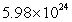 kg. Recall
kg. Recall 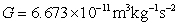 .
.
(Short Answer)
4.8/5  (37)
(37)
The position of a particle traversing a circular path is given by 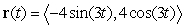 . Find the speed of the particle at time
. Find the speed of the particle at time 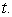
(Essay)
4.9/5  (45)
(45)
A projectile is fired form the ground at an angle of 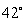 with an initial speed of 200 m/s. What is the velocity vector of the projectile after 11 seconds? Recall that
with an initial speed of 200 m/s. What is the velocity vector of the projectile after 11 seconds? Recall that 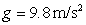 is the acceleration due to gravity on the Earth's surface. Approximate the components of your answer to the nearest tenth meter per second.
is the acceleration due to gravity on the Earth's surface. Approximate the components of your answer to the nearest tenth meter per second.
(Essay)
4.9/5  (36)
(36)
Find the arc length of the Archimedes spiral 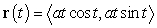 for
for 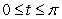 . Assume a is positive.
. Assume a is positive.
(Essay)
4.8/5  (36)
(36)
A path is parametrized by 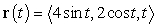 . Find the curvature of the path at the point
. Find the curvature of the path at the point 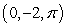 .
.
(Essay)
4.8/5  (29)
(29)
The curve 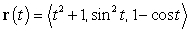 intersects the
intersects the 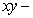 plane at which of the following points?
plane at which of the following points?
(Multiple Choice)
4.8/5  (44)
(44)
The path of a particle satisfies 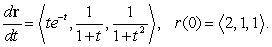 At
At 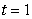 , the particle is located at:
, the particle is located at:
(Multiple Choice)
4.9/5  (38)
(38)
Consider the helix 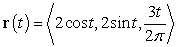 .
A) Find the unit tangent vector
.
A) Find the unit tangent vector 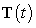 and the unit normal vector
and the unit normal vector 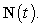 B) Find the curvature
B) Find the curvature 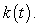
(Essay)
4.7/5  (28)
(28)
A particle has acceleration 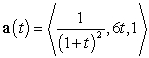 , initial velocity
, initial velocity 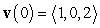 , and initial velocity
, and initial velocity 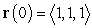 .
Decompose
.
Decompose 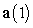 into tangential and normal components.
into tangential and normal components.
(Essay)
4.9/5  (32)
(32)
Consider the helix 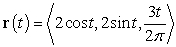 .
A) Compute the center and the radius of the osculating circle at
.
A) Compute the center and the radius of the osculating circle at 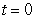 .
B) Compute the equation of the plane containing the osculating circle.
.
B) Compute the equation of the plane containing the osculating circle.
(Essay)
4.9/5  (48)
(48)
Let 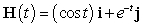 ,
, 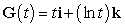 , and
, and 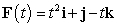 .
A) Compute
.
A) Compute 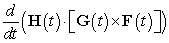 using the cross product and the dot product rules for differentiating.
A).
B) Compute the scalar triple product, differentiate it, and compare with the result in
using the cross product and the dot product rules for differentiating.
A).
B) Compute the scalar triple product, differentiate it, and compare with the result in
(Essay)
4.7/5  (32)
(32)
Showing 61 - 80 of 99
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)