Exam 7: Exponential Functions
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
From the top of a tall building, a 2-kg object is thrown vertically downward. One second after being thrown, the object has a velocity of 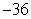 m/s. If the coefficient of air resistance is
m/s. If the coefficient of air resistance is 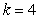 kg/s, what was the initial velocity of the object?
kg/s, what was the initial velocity of the object?
(Essay)
4.8/5  (39)
(39)
Find the domain on which 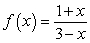 is one-to-one and a formula for the inverse of
is one-to-one and a formula for the inverse of 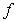 .
.
(Essay)
4.8/5  (40)
(40)
From the top of a tall building, a 5-kg object is thrown vertically downward. One second after it is thrown, the object has a velocity of 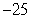 m/s. Two seconds after it is thrown, the object has a velocity of
m/s. Two seconds after it is thrown, the object has a velocity of 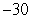 m/s. What was the initial velocity of the object?
m/s. What was the initial velocity of the object?
(Essay)
4.7/5  (32)
(32)
Find an equation of the tangent line to the graph of the function 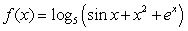 for
for 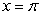 .
.
(Essay)
4.8/5  (38)
(38)
By Newton's Law of Cooling, an object in air cools down at a rate proportional to the difference between the object's temperature and the air temperature. When the air temperature is 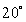 C, it takes 10 min for the object to cool down from
C, it takes 10 min for the object to cool down from 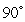 C to
C to 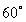 C. The temperature of the object decreases from
C. The temperature of the object decreases from 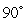 C to
C to 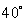 C during:
C during:
(Multiple Choice)
4.7/5  (35)
(35)
How long will it take for your money to double when it is invested at an annual rate of 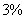 and compounded yearly? How long will it take for your money to double at an annual rate of
and compounded yearly? How long will it take for your money to double at an annual rate of 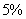 ?
?
(Short Answer)
4.8/5  (44)
(44)
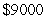 is deposited into an account earning interest at an annual rate of
is deposited into an account earning interest at an annual rate of 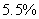 . Find the value of the account after one year if
A) it is compounded twice a year.
B) it is compounded monthly.
C) it is compounded weekly (52 weeks a year)
D) it is compounded daily (365 days a year)
E) it is compounded continuously.
Does the method of compounding have much effect on the final value?
. Find the value of the account after one year if
A) it is compounded twice a year.
B) it is compounded monthly.
C) it is compounded weekly (52 weeks a year)
D) it is compounded daily (365 days a year)
E) it is compounded continuously.
Does the method of compounding have much effect on the final value?
(Essay)
4.9/5  (36)
(36)
From the top of a tall building, a 1-kg object is thrown vertically downward. One second after being thrown, the object has a velocity of 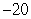 m/s. Two seconds after being thrown, the object has a velocity of
m/s. Two seconds after being thrown, the object has a velocity of 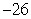 m/s. What is the coefficient of air resistance
m/s. What is the coefficient of air resistance 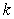 ?
?
(Essay)
4.8/5  (42)
(42)
A mug of hot chocolate with initial temperature 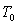 is placed on a table in a room held at
is placed on a table in a room held at 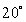 C. After 15 min, the temperature of the hot chocolate is
C. After 15 min, the temperature of the hot chocolate is 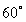 C. After an additional 30 min, the temperature of the hot chocolate is
C. After an additional 30 min, the temperature of the hot chocolate is 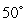 C. What was the initial temperature
C. What was the initial temperature 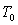 ?
?
(Essay)
4.9/5  (32)
(32)
The population of a country was 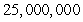 in 1980, whereas in 1990 it was
in 1980, whereas in 1990 it was 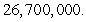 A) Find the population in
A) Find the population in 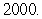 B) Determine the population's doubling time.
Assume that the rate of growth is proportional to the population.
B) Determine the population's doubling time.
Assume that the rate of growth is proportional to the population.
(Essay)
4.9/5  (32)
(32)
The decay constant of a 15-kg isotope is 0.137 (years) 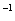 . Find the half-life of the isotope.
. Find the half-life of the isotope.
(Short Answer)
4.8/5  (29)
(29)
A population is modeled by a function 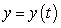 . Initially, the population counts 1000. The rate of change of the population is proportional to
. Initially, the population counts 1000. The rate of change of the population is proportional to 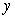 . Find the population at time
. Find the population at time 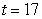 years given that the doubling time is 8 years.
years given that the doubling time is 8 years.
(Short Answer)
4.8/5  (37)
(37)
Showing 21 - 40 of 106
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)