Exam 9: First-Order Differential Equations
Exam 1: Preliminaries101 Questions
Exam 2: Limits and Continuity105 Questions
Exam 3: Differentiation116 Questions
Exam 4: Applications of the Derivative118 Questions
Exam 5: Integration129 Questions
Exam 6: Applications of the Definite Integral85 Questions
Exam 7: Exponentials, Logarithms and Other Transcendental Functions66 Questions
Exam 8: Integration Techniques123 Questions
Exam 9: First-Order Differential Equations72 Questions
Exam 10: Infinite Series111 Questions
Exam 11: Parametric Equations and Polar Coordinates129 Questions
Exam 12: Vectors and the Geometry of Space107 Questions
Exam 13: Vector-Valued Functions103 Questions
Exam 14: Functions of Several Variables and Partial Differentiation112 Questions
Exam 15: Multiple Integrals92 Questions
Exam 16: Vector Calculus67 Questions
Exam 17: Second Order Differential Equations38 Questions
Select questions type
Find all equilibrium points for the following coupled predator-prey-model equations. 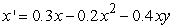
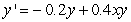
(Multiple Choice)
4.8/5  (47)
(47)
Consider a chemical system containing species A, B, and C; and that A and B can react to make C in a bimolecular reaction with rate constant of k1, and C can decompose to make A and B in a first order reaction with rate constant of k-1. If the instantaneous amounts of A, B, and C are represented as a, b, and c, and the initial amounts are given as A0, B0, and C0, the change in C can be represented with the differential equation ![Consider a chemical system containing species A, B, and C; and that A and B can react to make C in a bimolecular reaction with rate constant of k<sub>1</sub>, and C can decompose to make A and B in a first order reaction with rate constant of k<sub>-1</sub>. If the instantaneous amounts of A, B, and C are represented as a, b, and c, and the initial amounts are given as A<sub>0</sub>, B<sub>0</sub>, and C<sub>0</sub>, the change in C can be represented with the differential equation . If A<sub>0</sub> = 2 , B<sub>0</sub> = 2, C<sub>0</sub> = 0, k<sub>1</sub> = 0.04, and k<sub>-1</sub> = 0.04, solve the differential equation for c and graph the solution. [Note: c can never be larger than C<sub>0</sub> plus the smaller of A<sub>0</sub> or B<sub>0</sub>. Nor can it be smaller than 0.]](https://storage.examlex.com/TB5869/11eaa88b_9113_8f0e_a696_e18071ab97f7_TB5869_11.jpg) . If A0 = 2 , B0 = 2, C0 = 0, k1 = 0.04, and k-1 = 0.04, solve the differential equation for c and graph the solution. [Note: c can never be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]
. If A0 = 2 , B0 = 2, C0 = 0, k1 = 0.04, and k-1 = 0.04, solve the differential equation for c and graph the solution. [Note: c can never be larger than C0 plus the smaller of A0 or B0. Nor can it be smaller than 0.]
(Essay)
4.8/5  (39)
(39)
Use Euler's method with h = 0.1 to approximate y(1.0) and y(2.0) for the differential equation 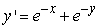 ,
, 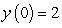 .
.
(Multiple Choice)
4.8/5  (33)
(33)
Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.] ![Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.]](https://storage.examlex.com/TB5869/11eaa88b_9115_b1fc_a696_29daeb5bed66_TB5869_11.jpg)
(Essay)
4.7/5  (30)
(30)
Solve the following initial value problem explicitly. 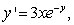 y(1) = -5
y(1) = -5
(Multiple Choice)
4.8/5  (33)
(33)
The Polymerase Chain Reaction (PCR) is used to replicate segments of DNA. It is used to make DNA samples big enough for testing, starting from very small samples collected, for instance, from a crime scene. PCR can double the number of a particular DNA segment every two minutes. Write an equation for the number of segments as a function of the number of minutes, t, if there is initially just one segment.
(Multiple Choice)
4.9/5  (41)
(41)
In 1965, Fairchild Semiconductor's R&D Director, Gordon Moore, noted that the maximum number of transistors that could be included cost effectively in one integrated circuit had been doubling yearly since 1959. While growth has not increased quite as quickly since 1965, it has still been exponential, and the continued exponential growth has become known as "Moore's Law". Considering that Intel's 4004 processor, introduced in 1971, had 2250 transistors, and their Pentium III processor, introduced in 1999, had 24,000,000 transistors, on average how long has it taken for processors to double the number of transistors they use.
(Multiple Choice)
4.9/5  (35)
(35)
An object falling freely through the atmosphere will accelerate due to the force of gravity at 9.86 m/s2 [Acceleration is the derivative of velocity with respect to time.] The atmosphere, however, will commonly exert a retarding force proportional to the object's velocity squared. The proportionality constant will depend largely on the object's shape. Write and solve the differential equation, then identify a free-falling object's terminal velocity (the limiting velocity) in terms of its drag proportionality constant, k. [To solve explicitly, you may use the initial condition v(0) = 0.]
(Essay)
4.8/5  (33)
(33)
Find the solution to the following separable differential equation. 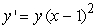
(Multiple Choice)
4.7/5  (33)
(33)
Use the direction field below to sketch a solution curve and estimate the initial value y(0) for the differential equation 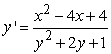 , such that the solution curve passes through the point (2, 2).
, such that the solution curve passes through the point (2, 2). 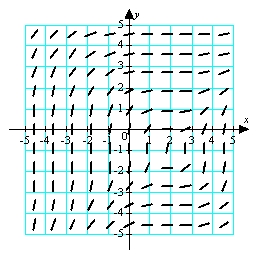
(Essay)
4.8/5  (39)
(39)
Find and interpret all equilibrium points for the competing species model. 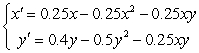
(Essay)
4.9/5  (41)
(41)
An object's cooling constant, k, is often taken to be proportional to the its surface area. An iron ball cools from 350oC to 100oC in 30 seconds in a fast flowing stream of 30oC water. Use Newton's Law of Cooling to estimate how cool a similar volume of hot iron would become in 30 seconds if it were in the shape of a rod with surface area 3 times larger than the ball's.
(Multiple Choice)
4.7/5  (39)
(39)
In 1995 an investor put $2500 in an account which paid 8%. In 2005 she withdrew $1500 from the account. What will the account be worth in 2020 ?
(Multiple Choice)
4.9/5  (39)
(39)
Find the solution to the following separable differential equation. 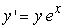
(Multiple Choice)
4.8/5  (35)
(35)
Find all equilibrium points for the following system of equations. 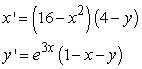
(Multiple Choice)
4.7/5  (43)
(43)
Showing 21 - 40 of 72
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)