Exam 9: First-Order Differential Equations
Exam 1: Preliminaries101 Questions
Exam 2: Limits and Continuity105 Questions
Exam 3: Differentiation116 Questions
Exam 4: Applications of the Derivative118 Questions
Exam 5: Integration129 Questions
Exam 6: Applications of the Definite Integral85 Questions
Exam 7: Exponentials, Logarithms and Other Transcendental Functions66 Questions
Exam 8: Integration Techniques123 Questions
Exam 9: First-Order Differential Equations72 Questions
Exam 10: Infinite Series111 Questions
Exam 11: Parametric Equations and Polar Coordinates129 Questions
Exam 12: Vectors and the Geometry of Space107 Questions
Exam 13: Vector-Valued Functions103 Questions
Exam 14: Functions of Several Variables and Partial Differentiation112 Questions
Exam 15: Multiple Integrals92 Questions
Exam 16: Vector Calculus67 Questions
Exam 17: Second Order Differential Equations38 Questions
Select questions type
The text describes logistic growth with an equation for the actual population in terms of a growth constant and a maximum population (carrying capacity), 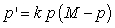 . The equation could also be written for a fraction of the maximum population in terms of a fractional growth constant. Re-express the differential equation in terms of the fractional population,
. The equation could also be written for a fraction of the maximum population in terms of a fractional growth constant. Re-express the differential equation in terms of the fractional population, 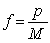 . Compare the time it takes for the population to go from 60% of the maximum to 80% of the maximum with the time it takes to go from 80% of the maximum to 90% of the maximum,
if k = 0.00020 day-1 and M = 5000?
. Compare the time it takes for the population to go from 60% of the maximum to 80% of the maximum with the time it takes to go from 80% of the maximum to 90% of the maximum,
if k = 0.00020 day-1 and M = 5000?
(Essay)
4.8/5  (41)
(41)
Match the appropriate slope field with the differential equation 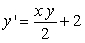 .
.
(Multiple Choice)
4.8/5  (32)
(32)
Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.] ![Use your calculator to construct the direction field for the following differential equation. [Use the standard zoom window.]](https://storage.examlex.com/TB5869/11eaa88b_9115_8aea_a696_2ffcf4fa2c6f_TB5869_11.jpg)
(Essay)
4.8/5  (46)
(46)
The differential equation is separable. Find the general solution in an explicit form. 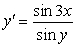
(Multiple Choice)
4.9/5  (36)
(36)
Find the solution of the differential equation, y' = -4y, satisfying the initial condition, y(0) = 7.
(Multiple Choice)
4.8/5  (40)
(40)
The number of stores in a particular chain of coffee bars was 200 in 1990 and began growing exponentially with a growth constant of 0.20 year-1. In what year would one predict the number of stores to reach 10,000?
(Multiple Choice)
4.8/5  (34)
(34)
The conversion of sucrose (table sugar) to glucose and fructose is first order in the concentration of sucrose, which means that the rate of reaction is proportional to the concentration of the sucrose. The rate of disappearance of sucrose can be expressed as 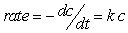 , where c represents the concentration of the sucrose, and k is called the rate constant and is mathematically identical to the negative of the decay constant. If the rate constant is 0.20 hour-1, how long will it take for the sucrose concentration to diminish to 1/80 of its initial concentration?
, where c represents the concentration of the sucrose, and k is called the rate constant and is mathematically identical to the negative of the decay constant. If the rate constant is 0.20 hour-1, how long will it take for the sucrose concentration to diminish to 1/80 of its initial concentration?
(Multiple Choice)
4.8/5  (43)
(43)
A volume discount on a certain item is expressed as a differential equation in which the derivative of the price per item with respect to the number purchased is proportional to the difference between the price and some base price, below which the price can never go. If the price for just one item is $60, and the base price is $30, and the price per item when buying 10 items is $54, what is the price per item when buying 100 items?
(Multiple Choice)
4.8/5  (26)
(26)
The rate at which water flows out of a drain in the bottom of a certain tank is proportional to the height of water in the tank. The tank is a vertical cylinder with cross-sectional area of 1.0 m2, so that every 1 cm in height represents 10 L. If the flow is 10 L/min (i.e. 1 cm/min) when the water level is 200 cm, how long will it take for the level to go from 200 cm to 20 cm?
(Multiple Choice)
4.8/5  (45)
(45)
Showing 61 - 72 of 72
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)