Exam 6: Applications of the Definite Integral
Exam 1: Preliminaries143 Questions
Exam 2: Limits and Continuity125 Questions
Exam 3: Differentiation150 Questions
Exam 4: Applications of the Derivative143 Questions
Exam 5: Integration154 Questions
Exam 6: Applications of the Definite Integral113 Questions
Exam 7: Integration Techniques95 Questions
Exam 8: First-Order Differential Equations72 Questions
Exam 9: Infinite Series111 Questions
Exam 10: Parametric Equations and Polar Coordinates129 Questions
Exam 11: Vectors and the Geometry of Space107 Questions
Exam 12: Vector-Valued Functions103 Questions
Exam 13: Functions of Several Variables and Partial Differentiation112 Questions
Exam 14: Multiple Integrals92 Questions
Exam 15: Vector Calculus67 Questions
Exam 16: Second Order Differential Equations38 Questions
Select questions type
Two divers, one on the 15 ft platform and one on the 30 ft platform, hope to perform a joint dive in which they enter the water at the same time. If each begins with an upward jump with an initial velocity of at 14 ft/s, how much time difference should there be between the start of the two dives?
(Multiple Choice)
4.8/5  (40)
(40)
The pdf describing the chance that a given insect will die at a particular age, x days, is 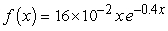 . What is the chance the insect will live longer than 6 days?
. What is the chance the insect will live longer than 6 days?
(Multiple Choice)
4.8/5  (37)
(37)
The moment of inertia, I, of an object is the second moment of its mass distribution relative to an axis of rotation, ![The moment of inertia, I, of an object is the second moment of its mass distribution relative to an axis of rotation, , where r is the perpendicular distance from the rotation axis and is the density of the object at a distance r from the rotation axis. What is the moment of inertia for rotation about the y-axis of a shape described by the region bordered by x = 0, and y = 0 revolved about the y-axis? Assume the density of the material is 1.0, so that mass and volume will be numerically equivalent. [Hint: Cylindrical shells are particularly conducive to moment-of-inertia calculations since r is everywhere the same for a given shell.]](https://storage.examlex.com/TB2342/11eaa948_cd0a_8748_84bc_017962db5af3_TB2342_11.jpg) , where r is the perpendicular distance from the rotation axis and
, where r is the perpendicular distance from the rotation axis and ![The moment of inertia, I, of an object is the second moment of its mass distribution relative to an axis of rotation, , where r is the perpendicular distance from the rotation axis and is the density of the object at a distance r from the rotation axis. What is the moment of inertia for rotation about the y-axis of a shape described by the region bordered by x = 0, and y = 0 revolved about the y-axis? Assume the density of the material is 1.0, so that mass and volume will be numerically equivalent. [Hint: Cylindrical shells are particularly conducive to moment-of-inertia calculations since r is everywhere the same for a given shell.]](https://storage.examlex.com/TB2342/11eaa948_cd0a_8749_84bc_dfbc31aa307b_TB2342_11.jpg) is the density of the object at a distance r from the rotation axis. What is the moment of inertia for rotation about the y-axis of a shape described by the region bordered by
is the density of the object at a distance r from the rotation axis. What is the moment of inertia for rotation about the y-axis of a shape described by the region bordered by ![The moment of inertia, I, of an object is the second moment of its mass distribution relative to an axis of rotation, , where r is the perpendicular distance from the rotation axis and is the density of the object at a distance r from the rotation axis. What is the moment of inertia for rotation about the y-axis of a shape described by the region bordered by x = 0, and y = 0 revolved about the y-axis? Assume the density of the material is 1.0, so that mass and volume will be numerically equivalent. [Hint: Cylindrical shells are particularly conducive to moment-of-inertia calculations since r is everywhere the same for a given shell.]](https://storage.examlex.com/TB2342/11eaa948_cd0a_874a_84bc_45db69b9ed50_TB2342_11.jpg) x = 0, and y = 0 revolved about the y-axis? Assume the density of the material is 1.0, so that mass and volume will be numerically equivalent. [Hint: Cylindrical shells are particularly conducive to moment-of-inertia calculations since r is everywhere the same for a given shell.]
x = 0, and y = 0 revolved about the y-axis? Assume the density of the material is 1.0, so that mass and volume will be numerically equivalent. [Hint: Cylindrical shells are particularly conducive to moment-of-inertia calculations since r is everywhere the same for a given shell.]
(Multiple Choice)
4.9/5  (34)
(34)
Find the volume of the solid with cross-sectional area 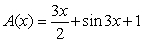 extending over the range
extending over the range 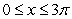 .
.
(Multiple Choice)
4.8/5  (39)
(39)
A water tower is spherical in shape with radius 35 feet, extending from 120 to 190 feet above ground. Compute the work done in filling the tank from the ground.
(Essay)
4.7/5  (31)
(31)
Identify the graph and area of the region bounded by the curves 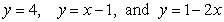 . The figures below are not necessarily to scale.
. The figures below are not necessarily to scale.
(Multiple Choice)
4.8/5  (32)
(32)
Find the area of the region determined by the intersections of the curves. 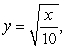
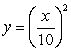
(Multiple Choice)
4.7/5  (40)
(40)
Use cylindrical shells to compute the volume of the solid formed by revolving the region bounded by 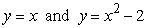 about x = 5.
about x = 5.
(Multiple Choice)
4.7/5  (31)
(31)
Find the volume of the solid formed by revolving the region bounded by 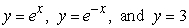 about y = 6.
about y = 6.
(Multiple Choice)
4.9/5  (38)
(38)
A cylindrical water tank has a radius of 2 feet and a height of 6.0 feet. Compute the work done to pump the water out of a filled tank through the top. [The density of water is 62.4 lbs/ft3.]
(Multiple Choice)
4.8/5  (31)
(31)
Find the length of the curve defined by function 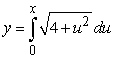 and extending from x = 0 to x = 2. Round your answer to three decimal places.
and extending from x = 0 to x = 2. Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (30)
(30)
Use the best method available to find the volume of the solid formed by revolving the region bounded by 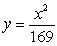 and
and 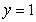 about the x-axis. Write the integral that is used to find the volume.
about the x-axis. Write the integral that is used to find the volume.
(Multiple Choice)
4.9/5  (37)
(37)
Find the area of the region bounded by the given curves. Write a single integral that represents the area. 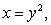
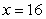
(Multiple Choice)
4.9/5  (31)
(31)
Identify the region (solid lines) and axis of revolution (dashed line) for the solid whose volume is described by the integral 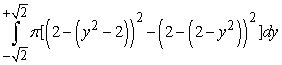 .
.
(Multiple Choice)
4.9/5  (32)
(32)
Use the best method available to find the volume of the solid formed by revolving the region bounded by 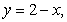
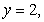 and
and 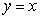 about the x-axis. Write the integral that is used to find the volume.
about the x-axis. Write the integral that is used to find the volume.
(Essay)
4.8/5  (33)
(33)
Sketch the region determined by the intersections of the curves. Estimate the intersection points to the nearest integer, then use these points to estimate the area. 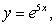
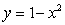
(Essay)
4.8/5  (29)
(29)
Showing 61 - 80 of 113
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)