Exam 6: Applications of the Definite Integral
Exam 1: Preliminaries143 Questions
Exam 2: Limits and Continuity125 Questions
Exam 3: Differentiation150 Questions
Exam 4: Applications of the Derivative143 Questions
Exam 5: Integration154 Questions
Exam 6: Applications of the Definite Integral113 Questions
Exam 7: Integration Techniques95 Questions
Exam 8: First-Order Differential Equations72 Questions
Exam 9: Infinite Series111 Questions
Exam 10: Parametric Equations and Polar Coordinates129 Questions
Exam 11: Vectors and the Geometry of Space107 Questions
Exam 12: Vector-Valued Functions103 Questions
Exam 13: Functions of Several Variables and Partial Differentiation112 Questions
Exam 14: Multiple Integrals92 Questions
Exam 15: Vector Calculus67 Questions
Exam 16: Second Order Differential Equations38 Questions
Select questions type
Magnetic hysteresis reflects the change in the magnetization, M, vs. applied field, H, when the applied field is increased then decreased in a cyclic fashion. The area between the M vs. H curves for increasing and decreasing H is related to the energy needed to take the material through the cycle. Use Simpson's rule on the M vs. H behavior listed in the table to calculate the area between the curves for the different directions of change of H. 
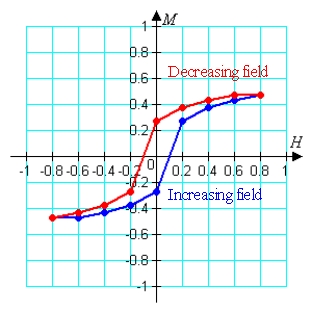
(Multiple Choice)
4.8/5  (39)
(39)
Use the best method available to find the volume of the solid formed by revolving the region bounded by the y-axis, 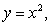
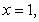 and
and 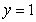 about the y-axis. Write the integral that is used to find the volume.
about the y-axis. Write the integral that is used to find the volume.
(Essay)
4.9/5  (42)
(42)
An object propelled from the ground with an initial velocity of 50 ft/s will reach a maximum height of 39.1 ft. If the initial velocity is increased 18%, by what percentage will the maximum height increase? Round percentages to the nearest integer.
(Multiple Choice)
4.8/5  (29)
(29)
Identify the initial conditions y(0) and y'(0) for the vertical motion of an object , if the object thrown downward at a velocity of 6 feet per second from a height of 30 feet. [Take the origin to be on the ground.]
(Multiple Choice)
4.8/5  (35)
(35)
Identify the integral used to determine the surface area of the surface of revolution for the shape described by 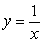 ,
, 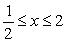 , revolved about the x-axis.
, revolved about the x-axis.
(Multiple Choice)
4.8/5  (31)
(31)
Identify the graph and area of the region bounded by the curves 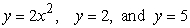 . Use only one integral. The figures below are not necessarily to scale.
. Use only one integral. The figures below are not necessarily to scale.
(Multiple Choice)
4.8/5  (33)
(33)
Use Simpson's Rule to estimate the volume of the shape obtained by revolving the cross-section given in the table about the y-axis. 
(Multiple Choice)
4.8/5  (38)
(38)
In a movie stunt, a car is driven off a cliff and falls into the ocean 200 feet below. If the car is going 50 feet/second (horizontally) when it goes over the cliff, its horizontal position is described as x = 50 t, where t is the time in seconds. Its vertical position is described as y = 16 t2, where y is the distance below the cliff (i.e. y = 200 when the car hits the ocean). Compute the length of the path traversed by the falling car. Round to the nearest foot. [Hint: The two equations will need to be combined, eliminating t so that y is expressed as a function of x.]
(Multiple Choice)
4.7/5  (30)
(30)
Let R be the region bounded by 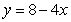 , the x-axis, and the y-axis. Compute the volume of the solid formed by revolving R about the x-axis.
, the x-axis, and the y-axis. Compute the volume of the solid formed by revolving R about the x-axis.
(Multiple Choice)
4.8/5  (37)
(37)
Compute the volume of a solid formed by revolving the region bounded by 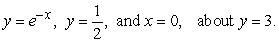
(Multiple Choice)
4.9/5  (39)
(39)
Identify the graph and the area of the region determined by the intersections of the tabulated curves using Simpson's Rule. 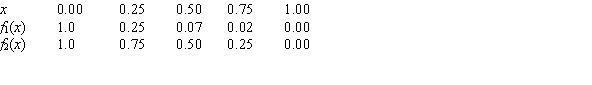
(Multiple Choice)
4.9/5  (37)
(37)
When a certain spring is stretched 0.10 m, 4 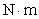 of work is done. What is the spring's "spring constant"?
of work is done. What is the spring's "spring constant"?
(Multiple Choice)
4.9/5  (36)
(36)
A baseball pitcher releases the ball horizontally from a height of 5 ft with an initial speed of 140 ft/s. Find the height of the ball when it reaches home plate 60 feet away. Round to two decimal places. (Hint: Determine the time of flight from the x-equation, then use the y-equation to determine the height.)
(Multiple Choice)
4.8/5  (29)
(29)
Use two straight line segments to estimate the length of the line segment described by the function 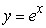 from
from 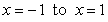 . Choose x = 0 as the middle point.
. Choose x = 0 as the middle point.
(Multiple Choice)
4.9/5  (44)
(44)
Find the median of x, given the pdf ![Find the median of x, given the pdf , . [Hint: Do not waste time trying to find an analytic solution. Once you determine the expression you would like to solve, just identify which of the choices is close to the correct answer.]](https://storage.examlex.com/TB2342/11eaa948_cd0c_5c38_84bc_3d814c7e53ec_TB2342_11.jpg) ,
, ![Find the median of x, given the pdf , . [Hint: Do not waste time trying to find an analytic solution. Once you determine the expression you would like to solve, just identify which of the choices is close to the correct answer.]](https://storage.examlex.com/TB2342/11eaa948_cd0c_5c39_84bc_0b810bb07ad3_TB2342_11.jpg) . [Hint: Do not waste time trying to find an analytic solution. Once you determine the expression you would like to solve, just identify which of the choices is close to the correct answer.]
. [Hint: Do not waste time trying to find an analytic solution. Once you determine the expression you would like to solve, just identify which of the choices is close to the correct answer.]
(Multiple Choice)
4.8/5  (24)
(24)
Find the value of c which will make the function 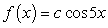 a pdf on the interval
a pdf on the interval 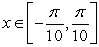 .
.
(Multiple Choice)
5.0/5  (38)
(38)
Sketch and find the area of the region determined by the intersections of the curves. 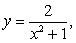
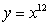
(Essay)
4.7/5  (41)
(41)
When pumping water out of a full hemispherical basin with radius r feet, how far down will the water level be when 1/5 of the work has been done? [The density of water is 62.4 lbs/ft3.]
(Multiple Choice)
4.9/5  (43)
(43)
Let R be the region bounded by 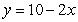 , the x-axis, and the y-axis. Compute the volume of the solid formed by revolving R about the y-axis.
, the x-axis, and the y-axis. Compute the volume of the solid formed by revolving R about the y-axis.
(Multiple Choice)
4.8/5  (39)
(39)
Showing 81 - 100 of 113
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)