Exam 10: A: Inference From Small Samples
Exam 1: Describing Data With Graphs134 Questions
Exam 2: Describing Data With Numerical Measures235 Questions
Exam 3: Describing Bivariate Data57 Questions
Exam 4: A: probability and Probability Distributions107 Questions
Exam 4: B: probability and Probability Distributions157 Questions
Exam 5: Several Useful Discrete Distributions166 Questions
Exam 6: The Normal Probability Distribution235 Questions
Exam 7: Sampling Distributions231 Questions
Exam 8: Large-Sample Estimation187 Questions
Exam 9: A: large-Sample Tests of Hypotheses154 Questions
Exam 9: B: large-Sample Tests of Hypotheses106 Questions
Exam 10: A: Inference From Small Samples192 Questions
Exam 10: B: Inference From Small Samples124 Questions
Exam 11: A: The Analysis of Variance136 Questions
Exam 11: B: The Analysis of Variance137 Questions
Exam 12: A: linear Regression and Correlation131 Questions
Exam 12: B: linear Regression and Correlation171 Questions
Exam 13: Multiple Regression Analysis232 Questions
Exam 14: Analysis of Categorical Data158 Questions
Exam 15: A:nonparametric Statistics139 Questions
Exam 15: B:nonparametric Statistics95 Questions
Select questions type
When small samples are used to estimate the true population mean where the population standard deviation is unknown, the margin of error for the confidence interval estimate tends to be very small.
(True/False)
4.8/5  (37)
(37)
If a sample of size 20 is randomly selected from a population, the value of A for the probability P(-A 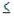 t
t 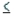 A) = 0.95 is 2.093.
A) = 0.95 is 2.093.
(True/False)
4.9/5  (33)
(33)
Which of the following may be used to describe the sampling distribution of the quantity 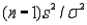 ?
?
(Multiple Choice)
4.9/5  (36)
(36)
Two independent samples are selected at random from two normal populations. The sample statistics are as follows: 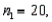
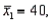
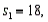
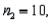
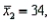 and
and 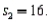 Assuming that a two-tailed hypothesis test is conducted at α = 0.05, what is the critical value?
Assuming that a two-tailed hypothesis test is conducted at α = 0.05, what is the critical value?
(Multiple Choice)
4.7/5  (33)
(33)
The t distribution allows the calculation of confidence intervals for means for small samples when the population variance is not known, regardless of the shape of the distribution in the population.
(True/False)
4.8/5  (35)
(35)
In testing 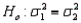 vs.
vs. 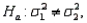 the critical value is determined from the F distribution table with an upper tail area equal to half the value of the level of significance.
the critical value is determined from the F distribution table with an upper tail area equal to half the value of the level of significance.
(True/False)
4.9/5  (45)
(45)
In testing 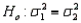 vs.
vs. 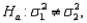 the null hypothesis will be rejected if the ratio
the null hypothesis will be rejected if the ratio 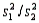 is substantially larger than 1.0.
is substantially larger than 1.0.
(True/False)
4.9/5  (35)
(35)
In constructing a 95% confidence interval estimate for the difference between the means of two normally distributed populations, where the unknown population variances are assumed NOT to be equal, summary statistics computed from two independent samples are as follows: 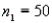 ,
, 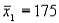 ,
, 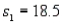 ,
, 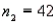 ,
, 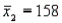 , and
, and 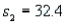 . In this case, what is the upper confidence limit?
. In this case, what is the upper confidence limit?
(Multiple Choice)
4.7/5  (35)
(35)
The test statistic used to test hypotheses about the population variance 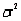 is
is 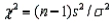 , which is chi-square distributed with n - 1 degrees of freedom when the population is normally distributed with variance equal to
, which is chi-square distributed with n - 1 degrees of freedom when the population is normally distributed with variance equal to 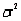 .
.
(True/False)
4.9/5  (40)
(40)
In testing 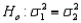 vs.
vs. 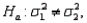 if
if 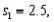 and
and 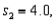 then the calculated value of the test statistic is F = 1.60.
then the calculated value of the test statistic is F = 1.60.
(True/False)
4.8/5  (36)
(36)
In a hypothesis test for a population variance 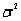 , the chi-square distribution is used to determine the critical value.
, the chi-square distribution is used to determine the critical value.
(True/False)
4.8/5  (26)
(26)
Which of the following distributions is used when testing 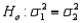 vs.
vs. 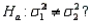
(Multiple Choice)
4.8/5  (25)
(25)
A random sample of size n has been selected from a normally distributed population. In hypothesis testing for the population mean, when should the t test be used instead of the z test?
(Multiple Choice)
4.8/5  (27)
(27)
The sampling distribution of the ratio of two sample variances 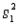 /
/ 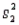 is said to be F distributed provided that the samples are dependent and their sizes are large.
is said to be F distributed provided that the samples are dependent and their sizes are large.
(True/False)
4.8/5  (32)
(32)
To estimate, with 95% confidence, the average number of kilometres that students living off-campus commute to classes every day, a random sample of 20 students was taken and produced a mean equal to 5.2 km and a standard deviation of 3.05 km. In this case, which of the following is the point estimate for the true population mean?
(Multiple Choice)
4.9/5  (40)
(40)
Which of the following characteristics must hold if the statistic 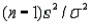 is to be chi-square distributed with n - 1 degrees of freedom?
is to be chi-square distributed with n - 1 degrees of freedom?
(Multiple Choice)
4.9/5  (36)
(36)
The F test used for testing the difference in two population variances is always a one-tailed test.
(True/False)
4.8/5  (28)
(28)
In testing 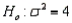 vs.
vs. 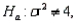 the following sample data were recorded: 5.0, 6.1, and 11.1. In this case, what is the value of the test statistic?
the following sample data were recorded: 5.0, 6.1, and 11.1. In this case, what is the value of the test statistic?
(Multiple Choice)
4.9/5  (29)
(29)
A political analyst in Manitoba surveys a random sample of registered Liberals and compares the results with those obtained from a random sample of registered Conservatives. This would be an example of an experimental design called a paired-difference or matched -pairs design.
(True/False)
4.9/5  (45)
(45)
Two samples of sizes 25 and 35 are independently drawn from two normal populations, where the unknown population variances are assumed to be equal. Which one of the following values is the number of degrees of freedom of the equal-variances t test statistic?
(Multiple Choice)
4.8/5  (36)
(36)
Showing 21 - 40 of 192
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)