Exam 10: A: Inference From Small Samples
Exam 1: Describing Data With Graphs134 Questions
Exam 2: Describing Data With Numerical Measures235 Questions
Exam 3: Describing Bivariate Data57 Questions
Exam 4: A: probability and Probability Distributions107 Questions
Exam 4: B: probability and Probability Distributions157 Questions
Exam 5: Several Useful Discrete Distributions166 Questions
Exam 6: The Normal Probability Distribution235 Questions
Exam 7: Sampling Distributions231 Questions
Exam 8: Large-Sample Estimation187 Questions
Exam 9: A: large-Sample Tests of Hypotheses154 Questions
Exam 9: B: large-Sample Tests of Hypotheses106 Questions
Exam 10: A: Inference From Small Samples192 Questions
Exam 10: B: Inference From Small Samples124 Questions
Exam 11: A: The Analysis of Variance136 Questions
Exam 11: B: The Analysis of Variance137 Questions
Exam 12: A: linear Regression and Correlation131 Questions
Exam 12: B: linear Regression and Correlation171 Questions
Exam 13: Multiple Regression Analysis232 Questions
Exam 14: Analysis of Categorical Data158 Questions
Exam 15: A:nonparametric Statistics139 Questions
Exam 15: B:nonparametric Statistics95 Questions
Select questions type
Both the equal-variances and the unequal-variances test statistics and confidence interval estimator of 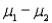 require that the two populations be normally distributed.
require that the two populations be normally distributed.
(True/False)
4.9/5  (35)
(35)
A random sample of size 9 produced a sample mean equal to 13.5 and a standard deviation of 3.2. The margin of error associated with a 95% confidence interval estimate for the population mean is approximately 2.46.
(True/False)
4.8/5  (36)
(36)
A random sample of size 15 taken from a normally distributed population revealed a sample mean of 75 and a sample variance of 25. What would the upper limit of a 95% confidence interval for the population mean equal?
(Multiple Choice)
4.8/5  (39)
(39)
The test statistic employed to test 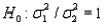 is
is 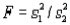 , which is F distributed with
, which is F distributed with 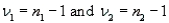 degrees of freedom, provided that the two populations are F distributed.
degrees of freedom, provided that the two populations are F distributed.
(True/False)
4.9/5  (32)
(32)
The necessary conditions having been met, a two-tailed test is being conducted at 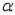 = 0.05 to test
= 0.05 to test 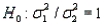 . The two sample variances are
. The two sample variances are 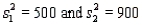 , and the sample sizes are
, and the sample sizes are 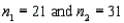 . The rejection region is F > 2.20 or F < 0.4255.
. The rejection region is F > 2.20 or F < 0.4255.
(True/False)
4.8/5  (39)
(39)
For 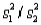 to have an F distribution, the variability of the measurements in the two populations must be the same and can be measured by a common variance,
to have an F distribution, the variability of the measurements in the two populations must be the same and can be measured by a common variance, 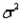 .
.
(True/False)
4.9/5  (36)
(36)
For an F distribution test statistic, the number of degrees of freedom associated with its denominator must be equal to the number of degrees of freedom associated with its numerator.
(True/False)
4.9/5  (38)
(38)
If you wish to test 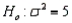 vs.
vs. 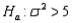 at the 0.05 level of significance using a sample of 15 observations, the critical value to be used is 23.685.
at the 0.05 level of significance using a sample of 15 observations, the critical value to be used is 23.685.
(True/False)
4.7/5  (43)
(43)
Which of the following best describes the Student's t distribution?
(Multiple Choice)
4.8/5  (42)
(42)
We are testing for the difference between the means of two independent populations with equal variances, and samples of 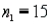 and
and 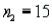 are taken. What does the number of degrees of freedom equal?
are taken. What does the number of degrees of freedom equal?
(Multiple Choice)
4.9/5  (31)
(31)
Matched pairs sampling may be used when testing the effectiveness of a new drug compared to a traditional one. Each patient in an experimental group might be matched with a partner in a control group of the same age, weight, height, sex, occupation, medical history, lifestyle, and so on.
(True/False)
4.8/5  (39)
(39)
In testing 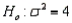 vs.
vs. 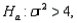 the following sample data were recorded: 11.5, 6.5, and 5.4. What is the p-value of the test?
the following sample data were recorded: 11.5, 6.5, and 5.4. What is the p-value of the test?
(Multiple Choice)
4.9/5  (38)
(38)
A random sample is selected from a normally distributed population. The following sample statistics are obtained: n = 20, 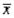 = 30, and s = 10. Based on this information, and using a 95% confidence level, which of the following is a valid calculation from the sample statistics?
= 30, and s = 10. Based on this information, and using a 95% confidence level, which of the following is a valid calculation from the sample statistics?
(Multiple Choice)
4.8/5  (43)
(43)
A random sample of 20 observations is selected from a normally distributed population. The sample variance is 12. What is the upper limit of the 95% confidence interval for the population variance?
(Multiple Choice)
4.8/5  (30)
(30)
An assumption behind the t distribution is that it assumes the population is normally distributed.
(True/False)
4.9/5  (34)
(34)
Two independent samples are selected at random from two normal populations. The sample statistics are as follows: 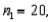
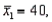
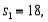
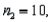
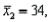 and
and 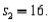 Assuming that a two-tailed hypothesis test is conducted at α = 0.05, what is the value of the test statistic?
Assuming that a two-tailed hypothesis test is conducted at α = 0.05, what is the value of the test statistic?
(Multiple Choice)
5.0/5  (26)
(26)
To estimate with 95% confidence the average number of kilometres that students living off-campus commute to classes every day, a random sample of 20 students was taken and produced a mean equal to 5.2 km and a standard deviation of 3.05 km. In this case, what would be the approximate value of the upper limit for a 95% confidence interval estimate for the true population mean?
(Multiple Choice)
4.8/5  (38)
(38)
The test for the equality of two population variances assumes that each of the two populations is normally distributed.
(True/False)
4.8/5  (36)
(36)
In testing for differences between the means of two independent populations, what is the null hypothesis?
(Multiple Choice)
4.9/5  (24)
(24)
Showing 81 - 100 of 192
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)