Exam 5: Several Useful Discrete Distributions

An oil firm plans to drill 20 wells, each having a probability 0.2 of striking oil. Each well costs $20,000 to drill; a well that strikes oil will bring in $750,000 in revenue. Find the expected gain from the 20 wells.

Intensive Care Unit Narrative The number x of people entering the intensive care unit at a particular hospital on any one day has a Poisson probability distribution with mean equal to four persons per day. -Refer to Intensive Care Unit Narrative. Is it likely that x will exceed ten? Explain.

Defective Items Narrative A random sample of 4 units is taken from a group of 15 items in which 4 units are known to be defective. Assume that sampling occurs without replacement, and the random variable x represents the number of defective units found in the sample. -Refer to Defective Items Narrative. What is P(x =3)?

A quiz consists of 15 multiple-choice questions. Each question has five choices, with exactly one correct choice. A student, totally unprepared for the quiz, guesses on each of the 15 questions. a. How many questions should the student expect to answer correctly? b. What is the standard deviation of the number of questions answered correctly? c. If at least nine questions must be answered correctly to pass the quiz, what is the chance the student passes?

A Canadian Medical Association study showed that 20% of all Canadians suffer from high blood pressure. Suppose we randomly sample ten Canadians to determine the number in the sample who have high blood pressure. a. What is the probability that, at most, two persons have high blood pressure? b. If, instead, we sampled 25 Canadians, give a reason why the following statement is true: "The probability between one and nine individuals from a sample of 25 would have high blood pressure is at least 0.75." [Hint: For n and p of approximately the sizes given, the distribution would not be particularly symmetric.]

Which of the following statements is a property of the binomial distribution?

A new surgical procedure is said to be successful 90% of the time. Suppose the operation is performed five times and the results are assumed to be independent of one another. Define x to be the number of successful operations. a. Find the probability that all five operations are successful. b. Find the probability that exactly four are successful. c. Find the probability that fewer than two are successful.

Computer Disks Narrative The quality of computer disks is measured by sending the disks through a certifier that counts the number of missing pulses. A certain brand of computer disks averages 0.1 missing pulses per disk. Let the random variable x denote the number of missing pulses. -Refer to Computer Disks Narrative. Find the probability that the next inspected disk will have no missing pulse.

Defective Items Narrative A random sample of 4 units is taken from a group of 15 items in which 4 units are known to be defective. Assume that sampling occurs without replacement, and the random variable x represents the number of defective units found in the sample. -Refer to Defective Items Narrative. Find P(x = 1).

The Poisson probability distribution is an example of a continuous probability distribution.

Scholarship Narrative A college has seven applicants for three scholarships: four females and three males. Suppose the seven applicants are equally qualified and no preference is given by the selection committee for choosing either gender. Let x equal the number of female students chosen for the three scholarships. -Refer to Scholarship Narrative. What is the probability that two females will receive a scholarship?

Toll Station Narrative It is known that between 8 and 10 a.m. on Saturdays, cars arrive at a certain toll station at a rate of 60 per hour. Assume that a Poisson process is occurring and that the random variable x represents the number of cars arriving at the station between 9:00 and 9:05 a.m. -Refer to Toll Station Narrative. Find P(x = 0).

Consider an experiment with 25 trials where the probability of success on any trial is 0.01, and let the random variable x be the number of successes among the 25 trials. What are p(0), p(1), p(2), and p(3) using the exact binomial distribution?

What is the standard deviation of a binomial distribution for which n = 50 and p = 0.15?

Which of these statements is NOT a property of a Poisson distribution?

Toll Station Narrative It is known that between 8 and 10 a.m. on Saturdays, cars arrive at a certain toll station at a rate of 60 per hour. Assume that a Poisson process is occurring and that the random variable x represents the number of cars arriving at the station between 9:00 and 9:05 a.m. -Refer to Toll Station Narrative. Find P(x = 10).

The number of successes observed during the n trials of a binomial experiment is called the binomial random variable.

The binomial random variable is the number of successes that occur in a certain period of time or space.

The number of traffic accidents per day on a certain section of highway is thought to be Poisson distributed with a mean equal to 2.19. Based on this, how many traffic accidents should be expected during a period of one week?

Let x be a hypergeometric random variable with N = 12, n = 4, and M = 3. a. Calculate p(0), p(1), p(2), and p(3). b. Construct the probability histogram for x. c. Calculate the mean 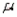and variance 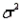. d. What proportion of the population of measurements fall into the interval 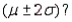Into the interval 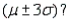Do these results agree with those given by Tchebysheff's Theorem?