Exam 5: Several Useful Discrete Distributions
Exam 1: Describing Data With Graphs134 Questions
Exam 2: Describing Data With Numerical Measures235 Questions
Exam 3: Describing Bivariate Data57 Questions
Exam 4: A: probability and Probability Distributions107 Questions
Exam 4: B: probability and Probability Distributions157 Questions
Exam 5: Several Useful Discrete Distributions166 Questions
Exam 6: The Normal Probability Distribution235 Questions
Exam 7: Sampling Distributions231 Questions
Exam 8: Large-Sample Estimation187 Questions
Exam 9: A: large-Sample Tests of Hypotheses154 Questions
Exam 9: B: large-Sample Tests of Hypotheses106 Questions
Exam 10: A: Inference From Small Samples192 Questions
Exam 10: B: Inference From Small Samples124 Questions
Exam 11: A: The Analysis of Variance136 Questions
Exam 11: B: The Analysis of Variance137 Questions
Exam 12: A: linear Regression and Correlation131 Questions
Exam 12: B: linear Regression and Correlation171 Questions
Exam 13: Multiple Regression Analysis232 Questions
Exam 14: Analysis of Categorical Data158 Questions
Exam 15: A:nonparametric Statistics139 Questions
Exam 15: B:nonparametric Statistics95 Questions
Select questions type
Telephone Switchboard Narrative
The number of telephone calls coming into a business's switchboard averages four calls per minute. Let x be the number of calls received.
-Refer to Telephone Switchboard Narrative. Find P(x = 0).
(Essay)
4.9/5  (34)
(34)
The Poisson parameter 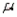 is the mean number of occurrences of an event per unit of time or space during the Poisson process.
is the mean number of occurrences of an event per unit of time or space during the Poisson process.
(True/False)
4.8/5  (29)
(29)
Telephone Switchboard Narrative
The number of telephone calls coming into a business's switchboard averages four calls per minute. Let x be the number of calls received.
-Refer to Telephone Switchboard Narrative. What is the probability at least one call will be received in a given two-minute period?
(Essay)
4.7/5  (42)
(42)
Toll Station Narrative
It is known that between 8 and 10 a.m. on Saturdays, cars arrive at a certain toll station at a rate of 60 per hour. Assume that a Poisson process is occurring and that the random variable x represents the number of cars arriving at the station between 9:00 and 9:05 a.m.
-Refer to Toll Station Narrative. What is the expected number of cars arriving at the toll station between 9:00 and 9:05 a.m.?
(Essay)
4.9/5  (35)
(35)
The number of defects in a random sample of 200 parts produced by a machine is binomially distributed with p = 0.03. Based on this information, the expected number of defects in the sample is six.
(True/False)
4.8/5  (43)
(43)
It is known that 70% of the customers in a sporting goods store purchase a pair of running shoes. A random sample of 25 customers is selected. Assume that customers' purchases are made independently, and let x represent the number of customers who purchase running shoes.
a. What is the probability that exactly 18 customers purchase running shoes?
b. What is the probability that no more than 19 customers purchase running shoes?
c. What is the probability that at least 17 customers purchase running shoes?
d. What is the probability that between 17 and 21 customers, inclusively, purchase running shoes?
(Essay)
4.9/5  (29)
(29)
Four in ten Canadians who travel by car look for gas and food outlets that are close to or visible from the highway. Suppose a random sample of n = 20 Canadians who travel by car are asked how they determine where to stop for food and gas. Let x be the number in the sample who respond that they look for gas and food outlets that are close to or visible from the highway.
a. What are the mean and variance of x?
b. Calculate the interval 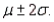 What values of the binomial random variable x fall into this interval?
c. Find
What values of the binomial random variable x fall into this interval?
c. Find 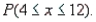 How does this compare with the fraction in the interval
How does this compare with the fraction in the interval 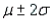 for any distribution? For mound-shaped distributions?
for any distribution? For mound-shaped distributions?
(Essay)
4.8/5  (31)
(31)
The hypergeometric probability distribution formula calculates the probability of x successes when a random sample of size n is drawn without replacement from a population of size N within which M units have the characteristic that denotes success, and N - M units have the characteristic that denotes failure.
(True/False)
4.9/5  (40)
(40)
A jug contains five black marbles and five white marbles well mixed. A marble is removed and its colour is noted. A second marble is removed, without replacing the first marble, and its colour is also noted. If x is the total number of black marbles in the two draws, then x has a binomial distribution.
(True/False)
4.8/5  (40)
(40)
Automobile Spark Plugs Narrative
An eight-cylinder automobile engine has two misfiring spark plugs. The mechanic removes all four plugs from one side of the engine.
-Refer to Automobile Spark Plugs Narrative. What is the variance of the number of misfiring spark plugs?
(Essay)
4.8/5  (34)
(34)
A psychiatrist believes that 90% of all people who visit doctors have s of a psychosomatic nature. She decides to select 25 patients at random to test her theory.
a. Assuming that the psychiatrist's theory is true, what is the expected value of x, the number of the 20 patients who have psychosomatic s?
b. What is the variance of x, assuming that the theory is true?
c. Find 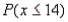 , assuming that the theory is true.
d. Based on the probability in (c), if only 14 of the 20 sampled had psychosomatic s, what conclusions would you make about the psychiatrist's theory? Explain.
, assuming that the theory is true.
d. Based on the probability in (c), if only 14 of the 20 sampled had psychosomatic s, what conclusions would you make about the psychiatrist's theory? Explain.
(Essay)
4.9/5  (28)
(28)
A statistics department is contacting alumni by telephone and asking for donations to help fund a new computer laboratory. Past history shows that 80% of the alumni contacted in this manner will make a contribution of at least $50. A random sample of 20 alumni is selected. Let x represent the number of alumni that make a contribution of at least $50.
a. What is the probability that exactly 15 alumni will make a contribution of at least $50?
b. What is the probability that between 14 and 18 alumni, inclusively, will make a contribution of at least $50?
c. What is the probability that fewer than 17 alumni will make a contribution of at least $50?
d. What is the probability that more than 15 alumni will make a contribution of at least $50?
e. How many alumni would you expect to make a contribution of at least $50?
(Essay)
5.0/5  (31)
(31)
Insulin-Dependent Diabetes Narrative
Insulin-dependent diabetes (IDD) is a common chronic disorder of children. Let us assume that an area in Europe has an incidence of 6 cases per 100,000 per year.
-Refer to Insulin-Dependent Diabetes Narrative. What is the probability that the number of cases is greater than or equal to 3 but less than or equal to 7 per 100,000?
(Essay)
4.8/5  (23)
(23)
A coin-toss experiment represents a binomial experiment only if the coin is balanced, meaning that p = 0.5.
(True/False)
4.8/5  (36)
(36)
Warehouse Narrative
A warehouse contains ten computer printers, four of which are defective. A company randomly selects five of the ten printers to purchase.
-Refer to Warehouse Narrative. What is the probability all five are non-defective?
(Essay)
4.8/5  (31)
(31)
Insulin-Dependent Diabetes Narrative
Insulin-dependent diabetes (IDD) is a common chronic disorder of children. Let us assume that an area in Europe has an incidence of 6 cases per 100,000 per year.
-Refer to Insulin-Dependent Diabetes Narrative. What is the probability that the number of cases of IDD in this area is less than or equal to 3 per 100,000?
(Essay)
4.8/5  (33)
(33)
Which of the following best describes our options when evaluating probabilities if we use the hypergeometric formula 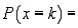
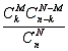 ?
?
(Multiple Choice)
4.7/5  (30)
(30)
Insulin-Dependent Diabetes Narrative
Insulin-dependent diabetes (IDD) is a common chronic disorder of children. Let us assume that an area in Europe has an incidence of 6 cases per 100,000 per year.
-Refer to Insulin-Dependent Diabetes Narrative. Would you expect to observe 10 or more cases of IDD per 100,000 in this area in a given year? Why or why not?
(Essay)
4.8/5  (39)
(39)
Hypergeometric probability distributions are examples of discrete probability distributions.
(True/False)
5.0/5  (24)
(24)
Given that n is the number of trials and p is the probability of success in any one trial of a random experiment, which of the following is equal to the expected value of a binomial random variable?
(Multiple Choice)
4.7/5  (30)
(30)
Showing 101 - 120 of 166
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)