Exam 4: B: probability and Probability Distributions
Exam 1: Describing Data With Graphs134 Questions
Exam 2: Describing Data With Numerical Measures235 Questions
Exam 3: Describing Bivariate Data57 Questions
Exam 4: A: probability and Probability Distributions107 Questions
Exam 4: B: probability and Probability Distributions157 Questions
Exam 5: Several Useful Discrete Distributions166 Questions
Exam 6: The Normal Probability Distribution235 Questions
Exam 7: Sampling Distributions231 Questions
Exam 8: Large-Sample Estimation187 Questions
Exam 9: A: large-Sample Tests of Hypotheses154 Questions
Exam 9: B: large-Sample Tests of Hypotheses106 Questions
Exam 10: A: Inference From Small Samples192 Questions
Exam 10: B: Inference From Small Samples124 Questions
Exam 11: A: The Analysis of Variance136 Questions
Exam 11: B: The Analysis of Variance137 Questions
Exam 12: A: linear Regression and Correlation131 Questions
Exam 12: B: linear Regression and Correlation171 Questions
Exam 13: Multiple Regression Analysis232 Questions
Exam 14: Analysis of Categorical Data158 Questions
Exam 15: A:nonparametric Statistics139 Questions
Exam 15: B:nonparametric Statistics95 Questions
Select questions type
Number of Cars Narrative
Let the random variable x represent the number of cars owned by a family. Assume that x can take on five values: 0, 1, 2, 3, 4. A partial probability distribution is shown below:  -From experience, a shipping company knows that the cost of delivering a small package within 24 hours is $16.20. The company charges $16.95 for shipment but guarantees to refund the charge if delivery is not made within 24 hours. If the company fails to deliver only 3% of its packages within the 24-hour period, what is the expected gain per package?
-From experience, a shipping company knows that the cost of delivering a small package within 24 hours is $16.20. The company charges $16.95 for shipment but guarantees to refund the charge if delivery is not made within 24 hours. If the company fails to deliver only 3% of its packages within the 24-hour period, what is the expected gain per package?
(Essay)
4.9/5  (37)
(37)
Drug Offenders Narrative
Research studies suggest that the likelihood a drug offender will be convicted of a drug offence within two years after treatment for drug abuse may depend on the person's educational level. The proportions of the total number of cases that fall into four education/conviction categories are shown in the table below:
Status within Two Years after Treatment 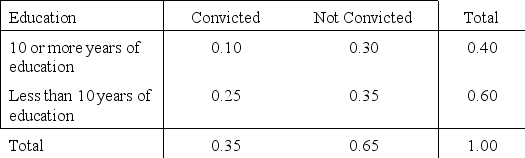 Suppose a single offender is selected from the treatment program. Here are two events of interest:
A: The offender has 10 or more years of education.
B: The offender is convicted within two years after completion of treatment.
-Refer to Drug Offenders Narrative. Find P
Suppose a single offender is selected from the treatment program. Here are two events of interest:
A: The offender has 10 or more years of education.
B: The offender is convicted within two years after completion of treatment.
-Refer to Drug Offenders Narrative. Find P 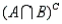 .
.
(Essay)
4.7/5  (34)
(34)
Job Applicants Narrative
Five applicants apply for two jobs. Applicants A and B are male; applicants C, D, and E are female. The personnel officer selects two applicants at random to fill the two jobs.
-A sample space S consists of five simple events with the following probabilities:
P( 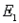 ) = P(
) = P( 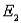 ) = 0.20, P(
) = 0.20, P( 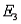 ) = 0.45, and P(
) = 0.45, and P( 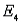 ) = 2P(
) = 2P( 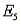 ).
a. Find the probabilities for simple events
).
a. Find the probabilities for simple events 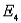 and
and 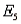 .
b. Find the probabilities for these two events: A:
.
b. Find the probabilities for these two events: A: 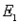 ,
, 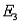 ,
, 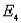 and B:
and B: 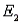 ,
, 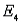 .
c. List the simple events that are in either event A or event B or both.
d. List the simple events that are in both event A and event B.
.
c. List the simple events that are in either event A or event B or both.
d. List the simple events that are in both event A and event B.
(Essay)
4.8/5  (34)
(34)
Random Selection of Marbles Narrative
A box contains one red, three blue, and two green marbles. Two marbles are randomly selected without replacement. Define events R, B, G, C, and D as follows:
R = {The selected marble is red.}
B = {The selected marble is blue.}
G = {The selected marble is green.}
C = {Both marbles selected are the same colour.}
D = {At least one of the marbles is blue.}
-Refer to Random Selection of Marbles Narrative. Find P(D).
(Essay)
4.8/5  (38)
(38)
Suppose that P(A) = 0.4, P(B) = 0.5, and that events A and B are mutually exclusive.
a. Find P(A 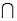 B).
b. Find P(A
B).
b. Find P(A 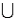 B).
B).
(Essay)
4.9/5  (40)
(40)
Smoking Habits of Health Club Members Narrative
A group of 40 people at a health club were classified according to their gender and smoking habits, as shown in the table below. One person is selected at random from that group of 40 people.
Smoking Habits 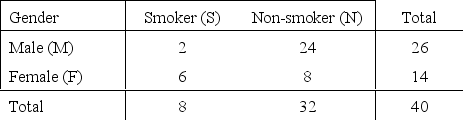 -Refer to Smoking Habits of Health Club Members Narrative. If the person is female, what is the probability she does not smoke?
-Refer to Smoking Habits of Health Club Members Narrative. If the person is female, what is the probability she does not smoke?
(Essay)
4.9/5  (39)
(39)
Number of Cars Narrative
Let the random variable x represent the number of cars owned by a family. Assume that x can take on five values: 0, 1, 2, 3, 4. A partial probability distribution is shown below:  -Refer to Number of Cars Narrative. Calculate the population mean, variance, and standard deviation.
-Refer to Number of Cars Narrative. Calculate the population mean, variance, and standard deviation.
(Essay)
4.8/5  (37)
(37)
An interior decorator must furnish two offices. Each office must have a desk, a chair, a file cabinet, and two bookcases. At a local office furniture store there are 6 models of desks, 8 models of chairs, 4 models of file cabinets, and 10 models of bookcases, all of which are compatible. (Any desk can be matched with any chair, etc.) How many choices does the decorator have if he wants to select 2 desks, 2 chairs, 2 file cabinets, and 4 bookcases but he doesn't want to select more than one of any model?
(Essay)
4.9/5  (35)
(35)
Number of Cars Narrative
Let the random variable x represent the number of cars owned by a family. Assume that x can take on five values: 0, 1, 2, 3, 4. A partial probability distribution is shown below:  -Refer to Number of Cars Narrative. What is the probability that that a family owns, at most, three cars?
-Refer to Number of Cars Narrative. What is the probability that that a family owns, at most, three cars?
(Essay)
4.9/5  (37)
(37)
Mall Shopper Narrative
One hundred shoppers at a local shopping mall were categorized by age and gender as shown in the frequency distribution below. One shopper is selected at random from that group of 100 shoppers.
Age Group 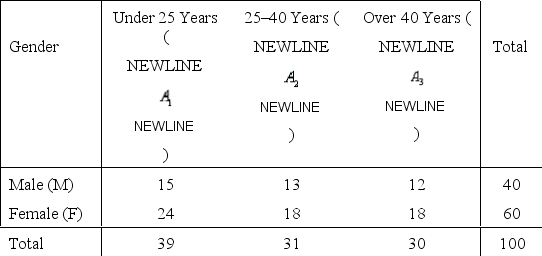 -Refer to Mall Shopper Narrative. Are the gender of the shopper and the shopper's age independent events? Explain.
-Refer to Mall Shopper Narrative. Are the gender of the shopper and the shopper's age independent events? Explain.
(Essay)
4.8/5  (39)
(39)
Population Samples Narrative
A sample is selected from one of two populations, 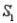 and
and 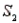 , with probabilities P(
, with probabilities P( 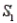 ) = 0.80 and P(
) = 0.80 and P( 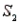 ) = 0.20. If the sample has been selected from
) = 0.20. If the sample has been selected from 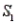 , the probability of observing an event A is P(A/
, the probability of observing an event A is P(A/ 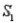 ) = 0.15. Similarly, If the sample has been selected from
) = 0.15. Similarly, If the sample has been selected from 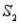 , the probability of observing A is P(A/
, the probability of observing A is P(A/ 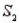 ) = 0.25.
-Refer to Population Samples Narrative. If a sample is randomly selected from one of the two populations, what is the probability that event A occurs?
) = 0.25.
-Refer to Population Samples Narrative. If a sample is randomly selected from one of the two populations, what is the probability that event A occurs?
(Essay)
4.8/5  (35)
(35)
Cheesecake Sales and Donations Narrative
The neighbourhood deli specializes in New York Style Cheesecake. The cheesecakes are made fresh daily and any unsold cheesecake is donated to a food bank. Each cheesecake costs $5 to make and sells for $11. The daily demand for cheesecake (the number the deli could sell if it had a cheesecake for everyone who wanted one) has the following distribution: 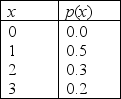 -Refer to Cheesecake Sales and Donations Narrative. What is the expected daily profit if the deli makes only one cheesecake per day?
-Refer to Cheesecake Sales and Donations Narrative. What is the expected daily profit if the deli makes only one cheesecake per day?
(Essay)
4.8/5  (28)
(28)
Random Selection of Marbles Narrative
A box contains one red, three blue, and two green marbles. Two marbles are randomly selected without replacement. Define events R, B, G, C, and D as follows:
R = {The selected marble is red.}
B = {The selected marble is blue.}
G = {The selected marble is green.}
C = {Both marbles selected are the same colour.}
D = {At least one of the marbles is blue.}
-Refer to Random Selection of Marbles Narrative. Find P(C 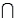 D).
D).
(Essay)
4.7/5  (35)
(35)
Drug Offenders Narrative
Research studies suggest that the likelihood a drug offender will be convicted of a drug offence within two years after treatment for drug abuse may depend on the person's educational level. The proportions of the total number of cases that fall into four education/conviction categories are shown in the table below:
Status within Two Years after Treatment  Suppose a single offender is selected from the treatment program. Here are two events of interest:
A: The offender has 10 or more years of education.
B: The offender is convicted within two years after completion of treatment.
-Refer to Drug Offenders Narrative. Find the probability of A given that B has occurred.
Suppose a single offender is selected from the treatment program. Here are two events of interest:
A: The offender has 10 or more years of education.
B: The offender is convicted within two years after completion of treatment.
-Refer to Drug Offenders Narrative. Find the probability of A given that B has occurred.
(Essay)
4.8/5  (42)
(42)
Working mothers in Canada
Statistics Canada wanted to find the distribution of ages of working women living in Canada who were single mothers. The researcher drew a random sample of some 300 families from the government tax records and found the following distribution:
Age Group 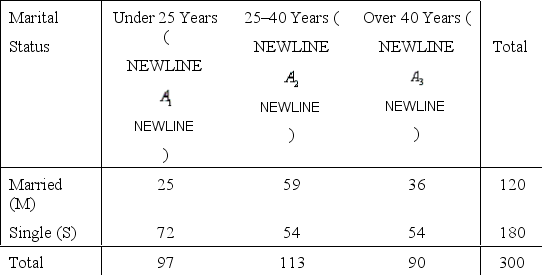 One family was selected at random from tax base records of families with working mothers.
-Refer to Working mothers in Canada. If the randomly selected working mother is married, what is the probability she is over 40 years of age?
One family was selected at random from tax base records of families with working mothers.
-Refer to Working mothers in Canada. If the randomly selected working mother is married, what is the probability she is over 40 years of age?
(Essay)
5.0/5  (33)
(33)
Psychological Tests Narrative
A psychologist tests Grade 7 students on basic word association skills and number pattern recognition skills. Let W be the event a student does well on the word association test. Let N be the event a student does well on the number pattern recognition test. A student is selected at random, and the following probabilities are given: P(W 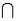 N) = 0.25, P(W
N) = 0.25, P(W 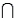
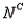 ) = 0.15, P(
) = 0.15, P( 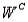
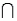 N) = 0.10, and P(
N) = 0.10, and P( 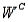
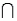
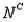 ) = 0.50.
-Refer to Psychological Tests Narrative. If the randomly selected student does well on the word association test, what is the probability he or she will also do well on the number pattern recognition test?
) = 0.50.
-Refer to Psychological Tests Narrative. If the randomly selected student does well on the word association test, what is the probability he or she will also do well on the number pattern recognition test?
(Essay)
4.8/5  (41)
(41)
Weight Gain for Calves Narrative
Let x denote the weight gain in kilograms per month for a calf. The probability distribution of x is shown below. 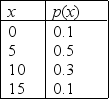 -Refer to Weight Gain for Calves Narrative. Find the average weight gain in kilograms per month for a calf.
-Refer to Weight Gain for Calves Narrative. Find the average weight gain in kilograms per month for a calf.
(Essay)
4.8/5  (34)
(34)
Dell Computer Owners Narrative
Dell computer owners are very faithful. Despite reporting s with their current systems, 90% of Dell owners said they would buy another computer from the company, based on the service they received. Suppose you randomly select three current Dell computer users and ask them whether they would buy another Dell computer system.
-Refer to Dell Computer Owners Narrative. Find the probability distribution for x, the number of Dell users in the sample of three who would buy another Dell computer.
(Essay)
4.9/5  (33)
(33)
Cheesecake Sales and Donations Narrative
The neighbourhood deli specializes in New York Style Cheesecake. The cheesecakes are made fresh daily and any unsold cheesecake is donated to a food bank. Each cheesecake costs $5 to make and sells for $11. The daily demand for cheesecake (the number the deli could sell if it had a cheesecake for everyone who wanted one) has the following distribution:  -Refer to Cheesecake Sales and Donations Narrative. What is the expected demand for cheesecake?
-Refer to Cheesecake Sales and Donations Narrative. What is the expected demand for cheesecake?
(Essay)
4.9/5  (39)
(39)
Typists' Errors Narrative
The random variable x is defined as the number of mistakes made by a typist on a randomly chosen page of a physics thesis. The probability distribution follows: 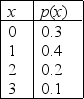 -Refer to Typists' Errors Narrative. Find
-Refer to Typists' Errors Narrative. Find 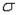 .
.
(Essay)
4.7/5  (23)
(23)
Showing 41 - 60 of 157
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)