Exam 4: B: probability and Probability Distributions
Exam 1: Describing Data With Graphs134 Questions
Exam 2: Describing Data With Numerical Measures235 Questions
Exam 3: Describing Bivariate Data57 Questions
Exam 4: A: probability and Probability Distributions107 Questions
Exam 4: B: probability and Probability Distributions157 Questions
Exam 5: Several Useful Discrete Distributions166 Questions
Exam 6: The Normal Probability Distribution235 Questions
Exam 7: Sampling Distributions231 Questions
Exam 8: Large-Sample Estimation187 Questions
Exam 9: A: large-Sample Tests of Hypotheses154 Questions
Exam 9: B: large-Sample Tests of Hypotheses106 Questions
Exam 10: A: Inference From Small Samples192 Questions
Exam 10: B: Inference From Small Samples124 Questions
Exam 11: A: The Analysis of Variance136 Questions
Exam 11: B: The Analysis of Variance137 Questions
Exam 12: A: linear Regression and Correlation131 Questions
Exam 12: B: linear Regression and Correlation171 Questions
Exam 13: Multiple Regression Analysis232 Questions
Exam 14: Analysis of Categorical Data158 Questions
Exam 15: A:nonparametric Statistics139 Questions
Exam 15: B:nonparametric Statistics95 Questions
Select questions type
Cheesecake Sales and Donations Narrative
The neighbourhood deli specializes in New York Style Cheesecake. The cheesecakes are made fresh daily and any unsold cheesecake is donated to a food bank. Each cheesecake costs $5 to make and sells for $11. The daily demand for cheesecake (the number the deli could sell if it had a cheesecake for everyone who wanted one) has the following distribution: 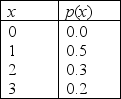 -Refer to Cheesecake Sales and Donations Narrative. What is the expected daily profit if the deli makes only two cheesecakes per day?
-Refer to Cheesecake Sales and Donations Narrative. What is the expected daily profit if the deli makes only two cheesecakes per day?
(Essay)
4.9/5  (42)
(42)
Late Night Talk Shows Narrative
Let A be the event that a randomly selected person watches the Tonight Show with Jay Leno (event A) and B be the event that a randomly selected person watches the Late Show with David Letterman (event B). It is possible to time-shift a program to a more convenient hour and thus watch both programs. Suppose the following probabilities are given: P(A 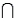 B) = 0.20, P(A
B) = 0.20, P(A 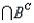 ) = 0.40, P(
) = 0.40, P( 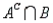 ) = 0.10, and P(
) = 0.10, and P( 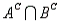 ) = 0.30.
-Refer to Late Night Talk Shows Narrative. If we know a person watches David Letterman, what is the probability he or she also watches Jay Leno?
) = 0.30.
-Refer to Late Night Talk Shows Narrative. If we know a person watches David Letterman, what is the probability he or she also watches Jay Leno?
(Essay)
4.9/5  (38)
(38)
Casino Card Game Narrative
The probability distribution of your winnings at a casino's card game is shown below. 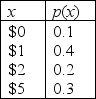 -Let x be a random variable with the following distribution:
-Let x be a random variable with the following distribution: 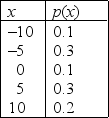 a. Find the expected value of x.
b. Find the standard deviation of x.
c. What is the probability that x is further than one standard deviation from the mean?
a. Find the expected value of x.
b. Find the standard deviation of x.
c. What is the probability that x is further than one standard deviation from the mean?
(Essay)
4.7/5  (34)
(34)
Late Night Talk Shows Narrative
Let A be the event that a randomly selected person watches the Tonight Show with Jay Leno (event A) and B be the event that a randomly selected person watches the Late Show with David Letterman (event B). It is possible to time-shift a program to a more convenient hour and thus watch both programs. Suppose the following probabilities are given: P(A 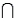 B) = 0.20, P(A
B) = 0.20, P(A 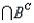 ) = 0.40, P(
) = 0.40, P( 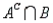 ) = 0.10, and P(
) = 0.10, and P( 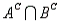 ) = 0.30.
-Refer to Late Night Talk Shows Narrative. If we know a person watches Jay Leno, what is the probability he or she also watches David Letterman?
) = 0.30.
-Refer to Late Night Talk Shows Narrative. If we know a person watches Jay Leno, what is the probability he or she also watches David Letterman?
(Essay)
4.7/5  (33)
(33)
Salary of Working Mothers Narrative
A researcher studied the relationship between the salary of a working woman with school-aged children and the number of children she had. The results are shown in the following probability table:
Number of Children  Let A denote the event that a working woman has two or fewer children, and let B denote the event that a working woman has a low salary.
-Refer to Salary of Working Mothers Narrative. What is the probability that a working woman either has two or fewer children or has a low salary?
Let A denote the event that a working woman has two or fewer children, and let B denote the event that a working woman has a low salary.
-Refer to Salary of Working Mothers Narrative. What is the probability that a working woman either has two or fewer children or has a low salary?
(Essay)
4.7/5  (41)
(41)
Psychological Tests Narrative
A psychologist tests Grade 7 students on basic word association skills and number pattern recognition skills. Let W be the event a student does well on the word association test. Let N be the event a student does well on the number pattern recognition test. A student is selected at random, and the following probabilities are given: P(W 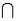 N) = 0.25, P(W
N) = 0.25, P(W 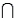
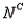 ) = 0.15, P(
) = 0.15, P( 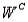
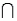 N) = 0.10, and P(
N) = 0.10, and P( 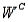
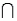
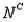 ) = 0.50.
-Refer to Psychological Tests Narrative. What is the probability that the randomly selected student does well on at least one of the tests?
) = 0.50.
-Refer to Psychological Tests Narrative. What is the probability that the randomly selected student does well on at least one of the tests?
(Essay)
4.9/5  (31)
(31)
Defective Bolts Narrative
Approximately 5% of the bolts coming off a production line have serious defects. Two bolts are randomly selected for inspection.
-Refer to Defective Bolts Narrative. Find E(x).
(Essay)
4.8/5  (33)
(33)
Casino Card Game Narrative
The probability distribution of your winnings at a casino's card game is shown below.  -Refer to Casino Card Game Narrative. How much should you expect to win if you play the game once?
-Refer to Casino Card Game Narrative. How much should you expect to win if you play the game once?
(Essay)
4.9/5  (39)
(39)
Population Samples Narrative
A sample is selected from one of two populations, 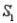 and
and 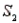 , with probabilities P(
, with probabilities P( 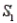 ) = 0.80 and P(
) = 0.80 and P( 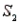 ) = 0.20. If the sample has been selected from
) = 0.20. If the sample has been selected from 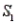 , the probability of observing an event A is P(A/
, the probability of observing an event A is P(A/ 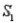 ) = 0.15. Similarly, If the sample has been selected from
) = 0.15. Similarly, If the sample has been selected from 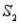 , the probability of observing A is P(A/
, the probability of observing A is P(A/ 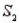 ) = 0.25.
-Refer to Population Samples Narrative. If a sample is randomly selected and event A is observed, what is the probability that the sample was selected from population
) = 0.25.
-Refer to Population Samples Narrative. If a sample is randomly selected and event A is observed, what is the probability that the sample was selected from population 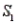 ? From population
? From population 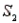 ?
?
(Essay)
4.8/5  (30)
(30)
Waste Management Project Narrative
A federal agency is trying to decide which of two waste management projects to investigate as the source of air pollution. In the past, projects of the first type were in violation of air quality standards with probability 0.3 on any given day, while projects of the second type were in violation of air quality standards with probability 0.25 on any given day. It is not possible for both projects to pollute the air in one day. Let 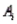 , i = 1, 2, denote that project of type i was in violation of air quality standards.
-Refer to Waste Management Project Narrative. If the first project is violating air quality standards, what is the probability the second project is also violating federal air quality standards?
, i = 1, 2, denote that project of type i was in violation of air quality standards.
-Refer to Waste Management Project Narrative. If the first project is violating air quality standards, what is the probability the second project is also violating federal air quality standards?
(Essay)
4.8/5  (34)
(34)
Number of Cars Narrative
Let the random variable x represent the number of cars owned by a family. Assume that x can take on five values: 0, 1, 2, 3, 4. A partial probability distribution is shown below:  -Refer to Number of Cars Narrative. What is the probability that a family owns more than two cars?
-Refer to Number of Cars Narrative. What is the probability that a family owns more than two cars?
(Short Answer)
4.9/5  (36)
(36)
Late Night Talk Shows Narrative
Let A be the event that a randomly selected person watches the Tonight Show with Jay Leno (event A) and B be the event that a randomly selected person watches the Late Show with David Letterman (event B). It is possible to time-shift a program to a more convenient hour and thus watch both programs. Suppose the following probabilities are given: P(A 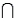 B) = 0.20, P(A
B) = 0.20, P(A 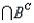 ) = 0.40, P(
) = 0.40, P( 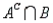 ) = 0.10, and P(
) = 0.10, and P( 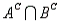 ) = 0.30.
-Refer to Late Night Talk Shows Narrative. What is the probability that a randomly selected person watches only David Letterman?
) = 0.30.
-Refer to Late Night Talk Shows Narrative. What is the probability that a randomly selected person watches only David Letterman?
(Essay)
4.8/5  (31)
(31)
Coffee Brands Narrative
A food company plans to conduct an experiment to compare its brand of coffee with that of two competitors. A single person is hired to taste each of three brands of coffee, which are unmarked except for identifying symbols, A, B, and C.
-Refer to Coffee Brands Narrative. If the taster has no ability to distinguish difference in taste among coffees, what is the probability that the taster will rank coffee type C as the most desirable? As the least desirable?
(Essay)
5.0/5  (33)
(33)
A graduate student has decided she needs a day at the beach. She will need a swimsuit, a pair of sunglasses, and a beach towel for the occasion. If she has two swimsuits, three pairs of sunglasses, and five beach towels, how many different choices does she have?
(Short Answer)
4.9/5  (32)
(32)
City Council Election Narrative
An election is being held to fill two city council seats. Two fiscally conservative candidates (denoted by C) and three small-L liberal candidates (denoted by L) are running for office. Assume the candidates are equally likely to be elected, and independent of each other.
-Refer to City Council Election Narrative. What are the possible outcomes of the election?
(Essay)
4.9/5  (38)
(38)
Psychological Tests Narrative
A psychologist tests Grade 7 students on basic word association skills and number pattern recognition skills. Let W be the event a student does well on the word association test. Let N be the event a student does well on the number pattern recognition test. A student is selected at random, and the following probabilities are given: P(W 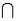 N) = 0.25, P(W
N) = 0.25, P(W 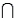
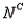 ) = 0.15, P(
) = 0.15, P( 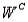
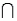 N) = 0.10, and P(
N) = 0.10, and P( 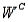
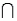
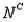 ) = 0.50.
-Refer to Psychological Tests Narrative. Are the events W and N independent? Explain.
) = 0.50.
-Refer to Psychological Tests Narrative. Are the events W and N independent? Explain.
(Essay)
4.7/5  (38)
(38)
Mall Shopper Narrative
One hundred shoppers at a local shopping mall were categorized by age and gender as shown in the frequency distribution below. One shopper is selected at random from that group of 100 shoppers.
Age Group 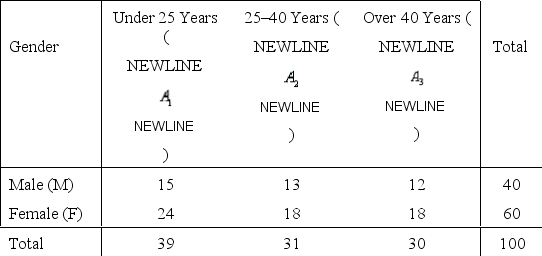 -Refer to Mall Shopper Narrative. What is the probability that the randomly selected shopper is either female or over 40 years of age?
-Refer to Mall Shopper Narrative. What is the probability that the randomly selected shopper is either female or over 40 years of age?
(Essay)
4.9/5  (44)
(44)
Smoking Habits of Health Club Members Narrative
A group of 40 people at a health club were classified according to their gender and smoking habits, as shown in the table below. One person is selected at random from that group of 40 people.
Smoking Habits 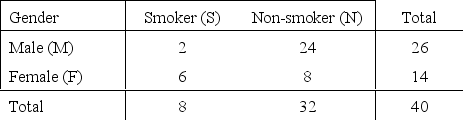 -Refer to Smoking Habits of Health Club Members Narrative. What is the probability the person does not smoke?
-Refer to Smoking Habits of Health Club Members Narrative. What is the probability the person does not smoke?
(Short Answer)
4.9/5  (37)
(37)
Working mothers in Canada
Statistics Canada wanted to find the distribution of ages of working women living in Canada who were single mothers. The researcher drew a random sample of some 300 families from the government tax records and found the following distribution:
Age Group 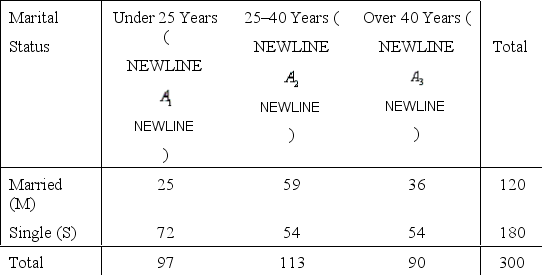 One family was selected at random from tax base records of families with working mothers.
-Refer to Working mothers in Canada. What is the probability that the randomly selected working mother is married?
One family was selected at random from tax base records of families with working mothers.
-Refer to Working mothers in Canada. What is the probability that the randomly selected working mother is married?
(Short Answer)
4.7/5  (36)
(36)
Salary of Working Mothers Narrative
A researcher studied the relationship between the salary of a working woman with school-aged children and the number of children she had. The results are shown in the following probability table:
Number of Children  Let A denote the event that a working woman has two or fewer children, and let B denote the event that a working woman has a low salary.
-Refer to Salary of Working Mothers Narrative. What is the probability that a working woman has a low salary?
Let A denote the event that a working woman has two or fewer children, and let B denote the event that a working woman has a low salary.
-Refer to Salary of Working Mothers Narrative. What is the probability that a working woman has a low salary?
(Short Answer)
4.9/5  (40)
(40)
Showing 101 - 120 of 157
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)