Exam 4: B: probability and Probability Distributions
Exam 1: Describing Data With Graphs134 Questions
Exam 2: Describing Data With Numerical Measures235 Questions
Exam 3: Describing Bivariate Data57 Questions
Exam 4: A: probability and Probability Distributions107 Questions
Exam 4: B: probability and Probability Distributions157 Questions
Exam 5: Several Useful Discrete Distributions166 Questions
Exam 6: The Normal Probability Distribution235 Questions
Exam 7: Sampling Distributions231 Questions
Exam 8: Large-Sample Estimation187 Questions
Exam 9: A: large-Sample Tests of Hypotheses154 Questions
Exam 9: B: large-Sample Tests of Hypotheses106 Questions
Exam 10: A: Inference From Small Samples192 Questions
Exam 10: B: Inference From Small Samples124 Questions
Exam 11: A: The Analysis of Variance136 Questions
Exam 11: B: The Analysis of Variance137 Questions
Exam 12: A: linear Regression and Correlation131 Questions
Exam 12: B: linear Regression and Correlation171 Questions
Exam 13: Multiple Regression Analysis232 Questions
Exam 14: Analysis of Categorical Data158 Questions
Exam 15: A:nonparametric Statistics139 Questions
Exam 15: B:nonparametric Statistics95 Questions
Select questions type
Weight Gain for Calves Narrative
Let x denote the weight gain in kilograms per month for a calf. The probability distribution of x is shown below. 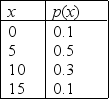 -Refer to Weight Gain for Calves Narrative. What is the probability that the variable x will lie strictly between 0 and 10 kilograms?
-Refer to Weight Gain for Calves Narrative. What is the probability that the variable x will lie strictly between 0 and 10 kilograms?
(Short Answer)
4.8/5  (38)
(38)
Mall Shopper Narrative
One hundred shoppers at a local shopping mall were categorized by age and gender as shown in the frequency distribution below. One shopper is selected at random from that group of 100 shoppers.
Age Group 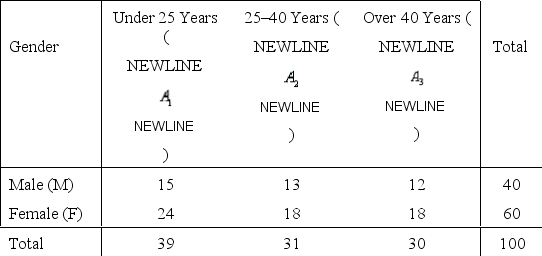 -Refer to Mall Shopper Narrative. If the randomly selected shopper is female, what is the probability that she is 25 to 40 years old?
-Refer to Mall Shopper Narrative. If the randomly selected shopper is female, what is the probability that she is 25 to 40 years old?
(Essay)
4.8/5  (34)
(34)
Weight Gain for Calves Narrative
Let x denote the weight gain in kilograms per month for a calf. The probability distribution of x is shown below.  -Refer to Weight Gain for Calves Narrative. What is P(0
-Refer to Weight Gain for Calves Narrative. What is P(0 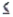 x
x 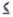 5)?
5)?
(Essay)
4.8/5  (31)
(31)
Late Night Talk Shows Narrative
Let A be the event that a randomly selected person watches the Tonight Show with Jay Leno (event A) and B be the event that a randomly selected person watches the Late Show with David Letterman (event B). It is possible to time-shift a program to a more convenient hour and thus watch both programs. Suppose the following probabilities are given: P(A 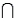 B) = 0.20, P(A
B) = 0.20, P(A 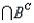 ) = 0.40, P(
) = 0.40, P( 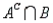 ) = 0.10, and P(
) = 0.10, and P( 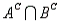 ) = 0.30.
-Refer to Late Night Talk Shows Narrative. What is the probability that a randomly selected person watches both shows?
) = 0.30.
-Refer to Late Night Talk Shows Narrative. What is the probability that a randomly selected person watches both shows?
(Essay)
4.7/5  (42)
(42)
Dell Computer Owners Narrative
Dell computer owners are very faithful. Despite reporting s with their current systems, 90% of Dell owners said they would buy another computer from the company, based on the service they received. Suppose you randomly select three current Dell computer users and ask them whether they would buy another Dell computer system.
-Refer to Dell Computer Owners Narrative. What is the probability that exactly one of the three Dell computer users would buy another Dell computer?
(Short Answer)
4.8/5  (42)
(42)
Typists' Errors Narrative
The random variable x is defined as the number of mistakes made by a typist on a randomly chosen page of a physics thesis. The probability distribution follows: 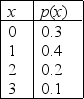 -Refer to Typists' Errors Narrative. In what fraction of pages in the thesis would the number of mistakes made be within two standard deviations of the mean?
-Refer to Typists' Errors Narrative. In what fraction of pages in the thesis would the number of mistakes made be within two standard deviations of the mean?
(Essay)
4.8/5  (46)
(46)
Drug Offenders Narrative
Research studies suggest that the likelihood a drug offender will be convicted of a drug offence within two years after treatment for drug abuse may depend on the person's educational level. The proportions of the total number of cases that fall into four education/conviction categories are shown in the table below:
Status within Two Years after Treatment 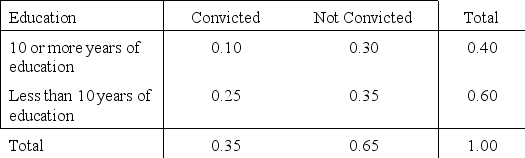 Suppose a single offender is selected from the treatment program. Here are two events of interest:
A: The offender has 10 or more years of education.
B: The offender is convicted within two years after completion of treatment.
-A missile designed to destroy enemy satellites has a 0.80 chance of destroying its target. If the government tests three missiles by firing them at a target, what is the probability all three fail to destroy the target? (Assume the missiles perform independently.)
Suppose a single offender is selected from the treatment program. Here are two events of interest:
A: The offender has 10 or more years of education.
B: The offender is convicted within two years after completion of treatment.
-A missile designed to destroy enemy satellites has a 0.80 chance of destroying its target. If the government tests three missiles by firing them at a target, what is the probability all three fail to destroy the target? (Assume the missiles perform independently.)
(Essay)
4.8/5  (42)
(42)
Working mothers in Canada
Statistics Canada wanted to find the distribution of ages of working women living in Canada who were single mothers. The researcher drew a random sample of some 300 families from the government tax records and found the following distribution:
Age Group 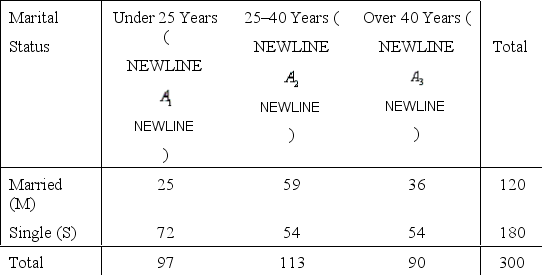 One family was selected at random from tax base records of families with working mothers.
-Refer to Working mothers in Canada. If the randomly selected working mother is between 25 and 40 years of age, what is the probability that she is single?
One family was selected at random from tax base records of families with working mothers.
-Refer to Working mothers in Canada. If the randomly selected working mother is between 25 and 40 years of age, what is the probability that she is single?
(Essay)
4.9/5  (26)
(26)
Job Applicants Narrative
Five applicants apply for two jobs. Applicants A and B are male; applicants C, D, and E are female. The personnel officer selects two applicants at random to fill the two jobs.
-Refer to Job Applicants Narrative. If the two jobs are different, and 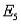 denotes the collection of outcomes where the successful job applicants include at least one female, what is P(
denotes the collection of outcomes where the successful job applicants include at least one female, what is P( 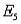 )?
)?
(Essay)
4.9/5  (42)
(42)
Fast-Food Restaurants Narrative
Lily frequents one of two fast-food restaurants, choosing McDonald's 25% of the time and Burger King 75% of the time. Regardless of where she goes, she buys french fries on 60% of her visits.
-Refer to Fast-Food Restaurants Narrative. What is the probability that Lily goes to McDonalds, or orders french fries, or both?
(Essay)
5.0/5  (30)
(30)
Weight Gain for Calves Narrative
Let x denote the weight gain in kilograms per month for a calf. The probability distribution of x is shown below.  -Refer to Weight Gain for Calves Narrative. Find the variance of the weight gain.
-Refer to Weight Gain for Calves Narrative. Find the variance of the weight gain.
(Essay)
5.0/5  (40)
(40)
Driver Education Narrative
Three randomly chosen 14-year-old middle school students who had not yet taken driver's education classes were given the written part of the Manitoba Driver's Exam. Each student was graded as passing (P) or failing (F) the written exam.
-Refer to Driver Education Narrative. Describe the sample space; that is, list all possible combinations of the three students' grades.
(Essay)
5.0/5  (31)
(31)
City Council Election Narrative
An election is being held to fill two city council seats. Two fiscally conservative candidates (denoted by C) and three small-L liberal candidates (denoted by L) are running for office. Assume the candidates are equally likely to be elected, and independent of each other.
-Refer to City Council Election Narrative. What is the probability both seats are filled by Conservatives?
(Short Answer)
4.8/5  (30)
(30)
Smoking and Gender Narrative
An experiment can result in one or both of events A = Smoker and B = Female, with the joint probabilities shown in the table below. A person is selected at random. 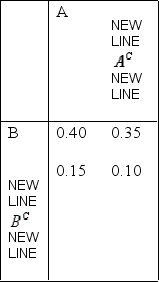 -Refer to Smoking and Gender Narrative. Find the probability that the person is a female smoker.
-Refer to Smoking and Gender Narrative. Find the probability that the person is a female smoker.
(Essay)
4.8/5  (32)
(32)
Smoking and Gender Narrative
An experiment can result in one or both of events A = Smoker and B = Female, with the joint probabilities shown in the table below. A person is selected at random.  -Refer to Smoking and Gender Narrative. Find the probability that the person is female.
-Refer to Smoking and Gender Narrative. Find the probability that the person is female.
(Essay)
4.8/5  (29)
(29)
SALES NARRATIVE
A salesperson either makes a sale (S) or does not make a sale (N) with each of two potential customers. The simple events and their probabilities are given below. 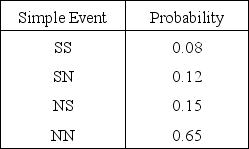 -Refer to Sales Narrative. What is the probability that at least one sale is made?
-Refer to Sales Narrative. What is the probability that at least one sale is made?
(Short Answer)
4.8/5  (39)
(39)
A businessman in Hamilton is preparing an itinerary for a visit to five major cities. Each city will be visited once and only once. The distance travelled, and hence the cost of the trip, will depend on the order in which he plans his route. How many different itineraries (and trip costs) are possible?
(Essay)
4.9/5  (32)
(32)
Showing 141 - 157 of 157
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)