Exam 2: Systems of Linear Equations and Matrices
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Find the sizes of A, B, C and D. 
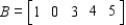
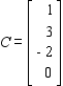
 A : __________ × __________ B : __________ × __________
C : __________ × __________ D : __________ × __________ ;
A : __________ × __________ B : __________ × __________
C : __________ × __________ D : __________ × __________ ;
(Short Answer)
4.7/5  (46)
(46)
Determine whether the system of linear equations has one and only one solution, infinitely many solutions, or no solution. Find all solutions whenever they exist. 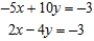
(Multiple Choice)
4.8/5  (40)
(40)
Find the inverse of the given matrix, if it exists. Verify your answer. 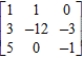
(Multiple Choice)
4.8/5  (45)
(45)
Jackson Farms have allotted a certain amount of land for cultivating soybeans, corn, and wheat. Cultivating 1 acre of soybeans requires 4 labor-hours, and cultivating 1 acre of corn or wheat requires 7 labor-hours. The cost of seeds for 1 acre of soybeans is $13, for 1 acre of corn is $20, and for 1 acre of wheat is $7. If all resources are to be used, how many acres of each crop should be cultivated if the following hold?
1,500 acres of land are allotted, 9,600 labor-hours are available, and $18,800 is available for seeds.
(Multiple Choice)
4.8/5  (33)
(33)
Writing a matrix equation that is equivalent to the given system of linear equations, solve the system using the inverse matrix. 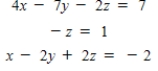
(Multiple Choice)
4.7/5  (28)
(28)
Formulate but do not solve the problem.
Michael Perez has a total of $1,500 on deposit with two savings institutions. One pays interest at the rate of 8%/year, whereas the other pays interest at the rate of 5%/year. If Michael earned a total of $96 in interest during a single year, how much does he have on deposit in each institution?
(Essay)
4.7/5  (39)
(39)
Find b13, b31 and b43. 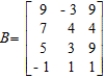 b13 = __________
b31 = __________
b43 = __________
b13 = __________
b31 = __________
b43 = __________
(Essay)
4.7/5  (36)
(36)
Writing the system of equations as a matrix equation solve the system of equations by using the inverse of the coefficient matrix. 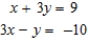
(Multiple Choice)
4.8/5  (40)
(40)
A dietitian wishes to plan a meal around three foods. The percent of the daily requirements of proteins, carbohydrates, and iron contained in each ounce of the three foods is summarized in the table. Determine how many ounces of each food the dietitian should include in the meal to meet exactly the daily requirement of proteins, carbohydrates, and iron (100% of each).  Food I: __________ ounces
Food II: __________ ounces
Food III: __________ ounces
Food I: __________ ounces
Food II: __________ ounces
Food III: __________ ounces
(Essay)
4.9/5  (31)
(31)
The relationship governing the intraindustrial and interindustrial sales and purchases of four basic industries - agriculture (A), manufacturing (M), transportation (T), and energy (E) - of a certain economy is given by the following input-output matrix. A M T E 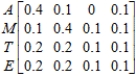 How many units of energy are required to produce 1 unit of manufacturing goods?
How many units of energy are required to produce 1 unit of manufacturing goods?
(Multiple Choice)
4.8/5  (31)
(31)
An executive of Trident Communications recently traveled to London, Paris, and Rome. He paid $190, $260, and $180/night for lodging in London, Paris, and Rome, respectively, and his hotel bills totaled $4,260. He spent $110, $140, and $90/day for his meals in London, Paris, and Rome, respectively, and his expenses for meals totaled $2,350. If he spent as many days in London as he did in Paris and Rome combined, how many days did he stay in each city?
__________ days in London
__________ days in Paris
__________ days in Rome
(Essay)
4.8/5  (32)
(32)
The total number of passengers riding a certain city bus during the morning shift is 900. If the child's fare is $.30, the adult fare is $.65, and the total revenue from the fares in the morning shift is 480, how many children and how many adults rode the bus during the morning shift?
(Multiple Choice)
4.9/5  (42)
(42)
Writing a matrix equation that is equivalent to the given system of linear equations solve the system using the inverse matrix.
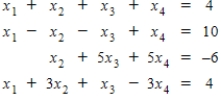
(Essay)
4.9/5  (31)
(31)
Company TKK Corporation, a large conglomerate, has three subsidiaries engaged in producing raw rubber, manufacturing tires, and manufacturing other rubber-based goods. The production of 1 unit of raw rubber requires the consumption of 0.08 unit of rubber, 0.05 unit of tires, and 0.02 unit of other rubber-based goods. To produce 1 unit of tires requires 0.5 unit of raw rubber, 0.09 unit of tires, and 0 units of other rubber-based goods. To produce 1 unit of other rubber-based goods requires 0.2 unit of raw rubber, 0.01 unit of tires, and 0.07 unit of other rubber-based goods. Market research indicates that the demand for the following year will be $400 million for raw rubber, $800 million for tires, and $180 million for other rubber-based products. Suppose the demand for raw rubber increases by 10%, the demand for tires increases by 20%, and the demand for other rubber-based products decreases by 10%. Find the level of production for each subsidiary in order to satisfy this demand. Round the answers to the nearest tenth, if necessary.
(Multiple Choice)
4.9/5  (26)
(26)
Indicate whether the matrix is in row-reduced form. Answer yes or no.

(Essay)
4.8/5  (33)
(33)
Solve the system of linear equations using the Gauss-Jordan elimination method. If there is no solution, answer none.
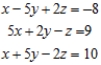
(Essay)
4.8/5  (23)
(23)
Given that the augmented matrix in row-reduced form is equivalent to the augmented matrix of a system of linear equations, determine whether the system has a solution and find the solution or solutions to the system, if they exist. If not, answer inconsistent. 
(Essay)
4.8/5  (31)
(31)
Showing 201 - 220 of 313
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)