Exam 2: Systems of Linear Equations and Matrices
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Matrix A is an input-output matrix associated with an economy, and matrix D (units in millions of dollars) is a demand vector. Find the final outputs of each industry so that the demands of both industry and the open sector are met.
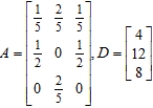
Round each answer to one decimal place, if necessary.
$__________ million output of the first sector
$__________ million output of the second sector
$__________ million output of the third sector
Round each answer to one decimal place, if necessary.
$__________ million output of the first sector
$__________ million output of the second sector
$__________ million output of the third sector
(Essay)
4.9/5  (30)
(30)
Solve the linear system of equations. If the system is inconsistent, indicate this.
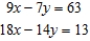
(Short Answer)
4.9/5  (41)
(41)
Let
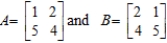
Compute AB and BA and hence deduce that matrix multiplication is, in general, not commutative.
Compute AB and BA and hence deduce that matrix multiplication is, in general, not commutative.


(Essay)
4.9/5  (38)
(38)
A simple economy consists of three sectors: agriculture (A), manufacturing (M), and transportation (T).The input-output matrix for this economy is given by
 Find the gross output of goods needed to satisfy a consumer demand for $100 million worth of agricultural products, $300 million worth of manufactured products, and $20 million worth of transportation. Round each number to two decimal places, if necessary.
$__________ million worth of agricultural products
$__________ million worth of manufactured goods
$__________ million worth of transportation
Find the gross output of goods needed to satisfy a consumer demand for $100 million worth of agricultural products, $300 million worth of manufactured products, and $20 million worth of transportation. Round each number to two decimal places, if necessary.
$__________ million worth of agricultural products
$__________ million worth of manufactured goods
$__________ million worth of transportation
(Essay)
4.7/5  (33)
(33)
Writing a matrix equation that is equivalent to the given system of linear equations solve the system using the inverse matrix. 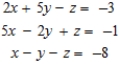
(Multiple Choice)
4.9/5  (31)
(31)
Determine whether the system of linear equations has one and only one solution, infinitely many solutions, or no solution. Find all solutions whenever they exist. 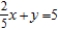
(Multiple Choice)
4.9/5  (31)
(31)
The relationship governing the intraindustrial and interindustrial sales and purchases of four basic industries - agriculture (A), manufacturing (M), transportation (T), and energy (E) - of a certain economy is given by the following input-output matrix.
A M T E 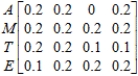 How many units of energy are required to produce 2 units of all goods in the economy?
__________ units
Which sector of the economy is least dependent on the cost of energy?
__________
How many units of energy are required to produce 2 units of all goods in the economy?
__________ units
Which sector of the economy is least dependent on the cost of energy?
__________
(Essay)
4.7/5  (43)
(43)
Given that the augmented matrix in row-reduced form is equivalent to the augmented matrix of a system of linear equations, determine whether the system has a solution and find the solution or solutions to the system, if they exist. 
(Multiple Choice)
4.8/5  (38)
(38)
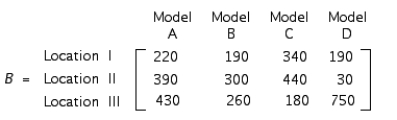
The total output of loudspeaker systems of the Acrosonic Company in their three production facilities for May and June is given by the matrices A and B, respectively, where 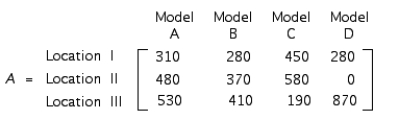
 The unit production costs and selling prices for these loudspeakers are given by matrices C and D, respectively, where
The unit production costs and selling prices for these loudspeakers are given by matrices C and D, respectively, where 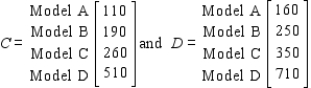 Calculate (A + B)(D - C).
Calculate (A + B)(D - C).
(Essay)
4.9/5  (41)
(41)
Bond Brothers, a real estate developer, builds houses in three states. The projected number of units of each model to be built in each state is given by the matrix 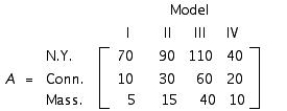 The profits to be realized are $20,000, $21,000, $26,000, and $30,000, respectively, for each model I, II, III, and IV house sold. Find the total profit Bond Brothers expects to earn in each state if all the houses are sold.
The profits to be realized are $20,000, $21,000, $26,000, and $30,000, respectively, for each model I, II, III, and IV house sold. Find the total profit Bond Brothers expects to earn in each state if all the houses are sold.
(Multiple Choice)
4.8/5  (20)
(20)
Find the inverse of the given matrix, if it exists. If not, write does not exist. Verify your answer.
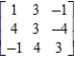
(Essay)
4.9/5  (29)
(29)
Identify the column matrix. What is its transpose? 
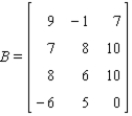
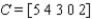
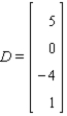 Column matrix: __________ (A,B,C or D)
Transpose: __________
Column matrix: __________ (A,B,C or D)
Transpose: __________
(Essay)
4.9/5  (24)
(24)
Cindy regularly makes long distance phone calls to three foreign cities: London, Tokyo, and Hong Kong. The matrices A and B give the lengths (in minutes) of her calls during peak and nonpeak hours, respectively, to each of these three cities during the month of June.  and
and  The costs for the calls (in dollars per minute) for the peak and nonpeak periods in the month in question are given, respectively, by the matrices
The costs for the calls (in dollars per minute) for the peak and nonpeak periods in the month in question are given, respectively, by the matrices 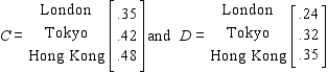 Compute the matrix
Compute the matrix 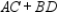 . Give the answer to one decimal place.
. Give the answer to one decimal place.
(Short Answer)
4.9/5  (28)
(28)
Let 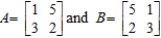 .
Compute AB and BA and hence deduce that matrix multiplication is, in general, not commutative.
.
Compute AB and BA and hence deduce that matrix multiplication is, in general, not commutative.
(Multiple Choice)
4.7/5  (32)
(32)
Consider a simple economy consisting of three sectors: food, clothing, and shelter. The production of 1 unit of food requires the consumption of 0.4 unit of food, 0.2 unit of clothing, and 0.4 unit of shelter. The production of 1 unit of clothing requires the consumption of 0.3 unit of food, 0.4 unit of clothing, and 0.1 unit of shelter. The production of 1 unit of shelter requires the consumption of 0.2 unit of food, 0.1 unit of clothing, and 0.2 unit of shelter. Find the level of production for each sector in order to satisfy the demand for $100 million worth of food, $30 million worth of clothing, and $290 million worth of shelter. Round the answers to the nearest tenth.
(Multiple Choice)
4.8/5  (35)
(35)
Matrix A is an input-output matrix associated with an economy, and matrix D (units in millions of dollars) is a demand vector. Find the final outputs of each industry so that the demands of both industry and the open sector are met. 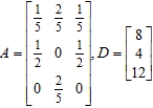
(Multiple Choice)
4.7/5  (36)
(36)
Find the inverse of the given matrix, if it exists. If not, write does not exist. Verify your answer.
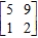
(Essay)
4.9/5  (38)
(38)
Write a matrix equation that is equivalent to the given system of linear equations and solve the system using the inverse matrix. 
(Multiple Choice)
4.9/5  (35)
(35)
Showing 241 - 260 of 313
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)