Exam 2: Systems of Linear Equations and Matrices
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
The relationship governing the intraindustrial and interindustrial sales and purchases of four basic industries - agriculture (A), manufacturing (M), transportation (T), and energy (E) - of a certain economy is given by the following input-output matrix.
A M T E 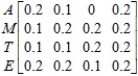 How many units of energy are required to produce 1 unit of manufacturing goods?
__________ units
Which sector of the economy has the smallest intra-industry purchases (sales)?
__________
How many units of energy are required to produce 1 unit of manufacturing goods?
__________ units
Which sector of the economy has the smallest intra-industry purchases (sales)?
__________
(Essay)
4.8/5  (38)
(38)
Solve the system of linear equations using the Gauss-Jordan elimination 
(Multiple Choice)
4.9/5  (35)
(35)
The annual interest on Sid Carrington's three investments amounted to $35,100: 6% on a savings account, 9% on mutual funds, and 12% on bonds. If the amount of Sid's investment in bonds was triple the amount of his investment in the savings account, and the interest earned from his investment in bonds was equal to the dividends he received from his investment in mutual funds, find how much money he placed in each type of investment.
(Multiple Choice)
4.9/5  (35)
(35)
Jackson Farms have allotted a certain amount of land for cultivating soybeans, corn, and wheat. Cultivating 1 acre of soybeans requires 4 labor-hours, and cultivating 1 acre of corn or wheat requires 7 labor-hours. The cost of seeds for 1 acre of soybeans is $12, for 1 acre of corn is $21, and for 1 acre of wheat is $9. If all resources are to be used, how many acres of each crop should be cultivated if the following hold?
1,200 acres of land are allotted, 7,200 labor-hours are available, and $19,200 is available for seeds.
acres of soybean: __________
acres of corn: __________
acres of wheat: __________
(Essay)
4.9/5  (35)
(35)
Solve the system of linear equations using the Gauss-Jordan elimination method. If there is no solution, answer none.
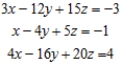
(Short Answer)
4.8/5  (30)
(30)
Solve the system of linear equations, using the Gauss-Jordan elimination method. 
(Multiple Choice)
4.8/5  (35)
(35)
Given that the augmented matrix in row-reduced form is equivalent to the augmented matrix of a system of linear equations, determine whether the system has a solution and find the solution or solutions to the system, if they exist. 
(Multiple Choice)
4.8/5  (33)
(33)
Solve the system of linear equations using the Gauss-Jordan elimination method. 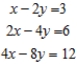
(Multiple Choice)
4.8/5  (27)
(27)
In this problem matrix A is an input-output matrix associated with an economy, and matrix D (units in millions of dollars) is a demand vector. Find the final outputs of each industry so that the demands of both industry and the open sector are met. 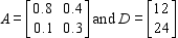
(Multiple Choice)
4.8/5  (38)
(38)
Solve the system of linear equations using the Gauss-Jordan elimination method. 
(Multiple Choice)
4.8/5  (28)
(28)
Formulate but do not solve the problem.
Kelly Fisher has a total of $32,000 invested in two municipal bonds that have yields of $5% and $6% interest per year, respectively. If the interest Kelly receives from the bonds in a year is $1,740, how much does she have invested in each bond?
(Essay)
4.7/5  (31)
(31)
Write the augmented matrix corresponding to the given system of equations. 
(Essay)
4.8/5  (35)
(35)
A simple economy consists of three sectors: agriculture (A), manufacturing (M), and transportation (T).The input-output matrix for this economy is given by A M T  Find the value of goods and transportation consumed in the internal process of production to satisfy a consumer demand for $100 million worth of agricultural products, $100 million worth of manufactured products, and $30 million worth of transportation.
Find the value of goods and transportation consumed in the internal process of production to satisfy a consumer demand for $100 million worth of agricultural products, $100 million worth of manufactured products, and $30 million worth of transportation.
(Multiple Choice)
4.9/5  (36)
(36)
A dietitian plans a meal around three foods. The number of units of vitamin A, vitamin C, and calcium in each ounce of these foods is represented by the matrix M, where  The matrices A and B represent the amount of each food (in ounces) consumed by a girl at two different meals, where
The matrices A and B represent the amount of each food (in ounces) consumed by a girl at two different meals, where 
 Calculate
Calculate 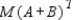 .
.
(Multiple Choice)
4.8/5  (38)
(38)
Showing 161 - 180 of 313
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)