Exam 2: Systems of Linear Equations and Matrices
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Solve the system of linear equations using the Gauss-Jordan elimination method. 
(Essay)
4.8/5  (31)
(31)
Solve the system of linear equations using the Gauss-Jordan elimination method. 
(Essay)
4.9/5  (36)
(36)
Solve the system of linear equations using the Gauss-Jordan elimination method. If there is no solution, answer none.
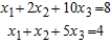
(Essay)
4.8/5  (30)
(30)
Determine whether the system of linear equations has one and only one solution, infinitely many solutions, or no solution. Find all solutions whenever they exist. 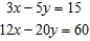
(Multiple Choice)
4.8/5  (32)
(32)
A university admissions committee anticipates an enrollment of 8,000 students in its freshman class next year. To satisfy admission quotas, incoming students have been categorized according to their sex and place of residence. The number of students in each category is given by the matrix

By using data accumulated in previous years, the admissions committee has determined that these students will elect to enter the College of Letters and Science, the College of Fine Arts, the School of Business Administration, and the School of Engineering according to the percentages that appear in the following matrix:
By using data accumulated in previous years, the admissions committee has determined that these students will elect to enter the College of Letters and Science, the College of Fine Arts, the School of Business Administration, and the School of Engineering according to the percentages that appear in the following matrix:
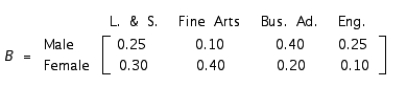
Find the matrix AB that shows the number of in-state, out-of-state, and foreign students expected to enter each discipline.
Find the matrix AB that shows the number of in-state, out-of-state, and foreign students expected to enter each discipline.
(Essay)
4.8/5  (41)
(41)
Solve the system of linear equations using the Gauss-Jordan elimination method. If there is no solution, answer none.
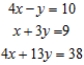
(Essay)
4.9/5  (30)
(30)
Solve the system of linear equations using the Gauss-Jordan elimination method. 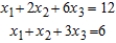
(Multiple Choice)
4.8/5  (32)
(32)
A system composed of two linear equations must have at least one solution if the straight lines represented by these equations are parallel.
(Multiple Choice)
4.9/5  (37)
(37)
Solve the system of linear equations, using the Gauss-Jordan elimination method. If there is no solution, answer none.
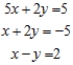
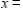 __________
__________
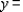 __________
__________
(Short Answer)
4.8/5  (35)
(35)
Solve the system of linear equations using the Gauss-Jordan elimination method. If there is no solution, answer none.
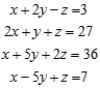
(Essay)
4.8/5  (30)
(30)
Write the augmented matrix corresponding to the given system of equations. 
(Essay)
4.9/5  (30)
(30)
Solve the system of linear equations using the Gauss-Jordan elimination method. 
(Essay)
4.9/5  (41)
(41)
Matrix A is an input-output matrix associated with an economy, and matrix D (units in millions of dollars) is a demand vector. Find the final outputs of each industry so that the demands of both industry and the open sector are met.

Round each answer to two decimal places, if necessary.
$__________ million output of the first sector
$__________ million output of the second sector
$__________ million output of the third sector
Round each answer to two decimal places, if necessary.
$__________ million output of the first sector
$__________ million output of the second sector
$__________ million output of the third sector
(Essay)
4.9/5  (35)
(35)
Write the augmented matrix corresponding to the given system of equations. 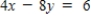
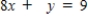
(Multiple Choice)
4.7/5  (36)
(36)
Matrix A gives the percentage of eligible voters in the city of Newton, classified according to party affiliation and age group. 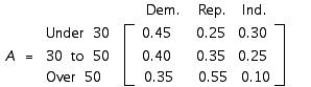 The population of eligible voters in the city by age group is given by the matrix B:
The population of eligible voters in the city by age group is given by the matrix B: 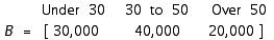 Find a matrix giving the total number of eligible voters in the city who will vote Democratic, Republican, and Independent.
Find a matrix giving the total number of eligible voters in the city who will vote Democratic, Republican, and Independent.
(Multiple Choice)
4.8/5  (40)
(40)
Showing 61 - 80 of 313
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)