Exam 2: Systems of Linear Equations and Matrices
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Solve the system of linear equations, using the Gauss-Jordan elimination method. 
(Multiple Choice)
4.8/5  (37)
(37)
The total output of loudspeaker systems of the Acrosonic Company in their three production facilities for May and June is given by the matrices A and B, respectively, where 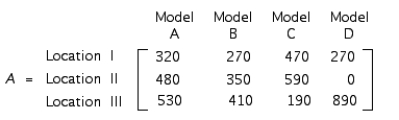
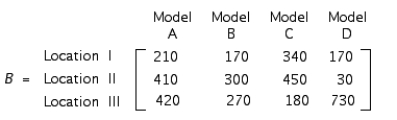 The unit production costs and selling prices for these loudspeakers are given by matrices C and D, respectively, where
The unit production costs and selling prices for these loudspeakers are given by matrices C and D, respectively, where 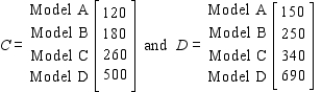 Calculate
Calculate 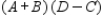 .
.
(Multiple Choice)
4.8/5  (39)
(39)
Given that the augmented matrix in rowreduced form is equivalent to the augmented matrix of a system of linear equations, find the solution or solutions to the system, if they exist. 
(Multiple Choice)
4.8/5  (41)
(41)
Formulate but do not solve the problem. The Coffee Shoppe sells a coffee blend made from two coffees, one costing $3.00/lb and the other costing $4.00/lb. If the blended coffee sells for $3.70/lb, find how much of each coffee is used to obtain the desired blend. (Assume the weight of the blended coffee is 100lb.) Let x be the weight of coffee with price $3.00/lb.
(Multiple Choice)
4.9/5  (27)
(27)
Formulate but do not solve the problem. The total number of passengers riding a certain city bus during the morning shift is 900. If the child's fare is $0.25, the adult fare is $0.75, and the total revenue from the fares in the morning shift is $475, how many children and how many adults rode the bus during the morning shift? Let x be the number of children.
(Multiple Choice)
4.9/5  (32)
(32)
Solve the system of linear equations using the Gauss-Jordan elimination method. 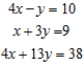
(Multiple Choice)
4.8/5  (33)
(33)
A simple economy consists of three sectors: agriculture (A), manufacturing (M), and transportation (T). The input-output matrix for this economy is given by
A M T  If the units are measured in millions of dollars, determine the dollar amount of manufactured products required to produce $200 million worth of all goods in the economy.
$__________ million
Which sector(s) consumes the greatest amount of agricultural products in the production of a unit of goods in that sector?
__________
Which sector(s) consumes the least amount of agricultural products in the production of a unit of goods in that sector?
__________
If the units are measured in millions of dollars, determine the dollar amount of manufactured products required to produce $200 million worth of all goods in the economy.
$__________ million
Which sector(s) consumes the greatest amount of agricultural products in the production of a unit of goods in that sector?
__________
Which sector(s) consumes the least amount of agricultural products in the production of a unit of goods in that sector?
__________
(Essay)
4.8/5  (38)
(38)
Write a matrix equation that is equivalent to the system of linear equations and solve the system. 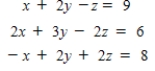
(Multiple Choice)
4.9/5  (38)
(38)
A simple economy consists of two industries: agriculture and manufacturing. The production of 1 unit of agricultural products requires the consumption of 0.4 unit of agricultural products and 0.2 unit of manufactured goods. The production of 1 unit of manufactured products requires the consumption of 0.3 unit of agricultural products and 0.3 unit of manufactured goods.
Find the value of the goods consumed in the internal process of production needed to satisfy a consumer demand for $150 million worth of agricultural products and $150 million worth of manufactured products. Round answers to two decimal places, if necessary.
$__________ million worth of agricultural goods
$__________ million worth of manufactured products.
(Essay)
4.9/5  (36)
(36)
Solve the matrix equation 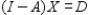 for the given matrices A, D and X.
for the given matrices A, D and X.
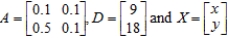
Round each answer to two decimal places, if necessary.
x = __________
y = __________
Round each answer to two decimal places, if necessary.
x = __________
y = __________
(Essay)
4.9/5  (34)
(34)
Formulate but do not solve the problem. The management of Hartman Rent-A-Car has allocated $1.5 million to buy a fleet of new automobiles consisting of compact, intermediate-size, and full size cars. Compacts cost $13,202 each, intermediate-size cars cost $28,827 each, and full-size cars cost $36,854 each. If Hartman purchases twice as many compacts as intermediate-size cars and the total number of cars to be purchased is 128, determine how many cars of each type will be purchased.(Assume that the entire budget will be used.) Let x be the number of compact, y be the number of intermediate-size cars, z be the number of full-size cars.
(Multiple Choice)
4.8/5  (32)
(32)
The Johnson Farm has 700 acres of land allotted for cultivating corn and wheat. The cost of cultivating corn and wheat (including seeds and labor) is $41 and $34/acre, respectively. Jacob Johnson has $25,900 available for cultivating these crops. If he wishes to use all the allotted land and his entire budget for cultivating these two crops, how many acres of each crop should he plant?
__________ acres of corn
__________ acres of wheat
(Essay)
4.8/5  (32)
(32)
Rainbow Harbor Cruises charges $10/adult and $5/child for a round-trip ticket. The records show that, on a certain weekend, 1,000 people took the cruise on Saturday and 1,200 people took the cruise on Sunday. The total receipts for Saturday were $7,000, and the total receipts for Sunday were $10,500. Determine how many adults and children took the cruise on Saturday and on Sunday.
Saturday: _____ adults, _____ children; Sunday: _____ adults, _____children.
(Essay)
4.9/5  (30)
(30)
Showing 181 - 200 of 313
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)