Exam 2: Systems of Linear Equations and Matrices
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Determine whether the system of linear equations has one and only one solution, infinitely many solutions, or no solution. Find all solutions whenever they exist. 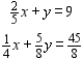
(Essay)
4.9/5  (29)
(29)
Write the system of equations corresponding to the given augmented matrix.
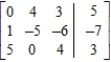
(Essay)
4.8/5  (32)
(32)
Solve the system of linear equations, using the Gauss-Jordan elimination method. If there is no solution, answer none.
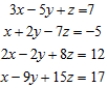
 __________
__________
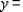 __________
__________
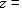 __________
__________
(Essay)
4.9/5  (31)
(31)
The accompanying figure shows the flow of traffic near a city's Civic Center during the rush hours on a typical weekday. Each road can handle a maximum of 1,000 cars/hour without causing congestion. The flow of traffic is controlled by traffic lights at each of the five intersections.  Set up a system of linear equations describing the traffic flow and solve this system.
Set up a system of linear equations describing the traffic flow and solve this system.
(Essay)
4.8/5  (38)
(38)
Mr. and Mrs. Garcia have a total of $200,000 to be invested in stocks, bonds, and a money market account. The stocks have a rate of return of 11%/year, while the bonds and the money market account pay 9% and 3%/year, respectively. They have stipulated that the amount invested in stocks should be equal to the sum of the amount invested in bonds and 7 times the amount invested in the money market account. How should the Garcias allocate their resources if they require an annual income of $20,000 from their investments?
(Multiple Choice)
5.0/5  (37)
(37)
Determine whether the system of linear equations has one and only one solution, infinitely many solutions, or no solution. Find all solutions whenever they exist.
(Essay)
4.9/5  (30)
(30)
Find the inverse of the given matrix, if it exists. If not, write does not exist. Verify your answer.
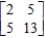
(Essay)
4.9/5  (28)
(28)
Solve the system of linear equations using the Gauss-Jordan elimination method. If there is no solution, answer none.
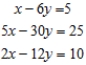
(Essay)
4.8/5  (42)
(42)
Lawnco produces three grades of commercial fertilizers. A 100-lb bag of grade A fertilizer contains 36 lb of nitrogen, 8 lb of phosphate, and 10 lb of potassium. A 100-lb bag og grade B fertilizer contains 40 lb of nitrogen and 8 lb of phosphate and 8 potassium. A 100-lb bag of grade C fertilizer contains 48 lb of nitrogen, 6 lb of phosphate, and 12 lb of potassium. How many 100-lb bags of each of the three grades of fertilizer should Lawnco procedure if 26,400 lb of nitrogen, 4,900 lb of phosphate, and 6,200 lb of potassium are available and all the nutrients are used?
(Multiple Choice)
4.7/5  (37)
(37)
Writing a matrix equation that is equivalent to the given system of linear equations, solve the system using the inverse matrix.
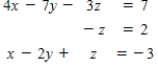
(Essay)
4.9/5  (41)
(41)
Find the inverse of the given matrix, if it exists. Verify your answer. 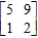
(Multiple Choice)
4.8/5  (30)
(30)
Lawnco produces three grades of commercial fertilizers. A 100-lb bag of grade-A fertilizer contains 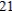 lb of nitrogen,
lb of nitrogen,  lb of phosphate, and
lb of phosphate, and 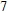 lb of potassium. A 100-lb bag of grade-B fertilizer contains
lb of potassium. A 100-lb bag of grade-B fertilizer contains 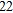 lb of nitrogen and
lb of nitrogen and  lb each of phosphate and potassium. A 100-lb bag of grade-C fertilizer contains
lb each of phosphate and potassium. A 100-lb bag of grade-C fertilizer contains 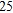 lb of nitrogen,
lb of nitrogen,  lb of phosphate, and
lb of phosphate, and  lb of potassium. How many 100-lb bags of each of the three grades of fertilizers should Lawnco produce if
lb of potassium. How many 100-lb bags of each of the three grades of fertilizers should Lawnco produce if 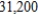 lb of nitrogen,
lb of nitrogen, 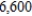 lb of phosphate, and
lb of phosphate, and 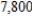 lb of potassium are available and all the nutrients are used?
grade-A fertilizer: __________ 100-lb bags
grade-B fertilizer: __________ 100-lb bags
grade-C fertilizer: __________ 100-lb bags
lb of potassium are available and all the nutrients are used?
grade-A fertilizer: __________ 100-lb bags
grade-B fertilizer: __________ 100-lb bags
grade-C fertilizer: __________ 100-lb bags
(Essay)
4.8/5  (37)
(37)
Solve the system of linear equations using the Gauss-Jordan elimination method. 
(Essay)
4.8/5  (34)
(34)
Writing a matrix equation that is equivalent to the given system of linear equations solve the system using the inverse matrix. 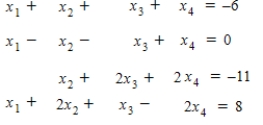
(Multiple Choice)
4.7/5  (31)
(31)
Showing 261 - 280 of 313
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)