Exam 14: Markov Analysis

Which of the following is not an assumption of Markov processes?

Three fast food hamburger restaurants are competing for the college lunch crowd.Burger Bills has 40% of the market while Hungry Heifer and Salty Sams each have 30% of the market.Burger Bills loses 10% of its customers to Hungry Heifer and 10% to Salty Sams each month.Hungry Heifer loses 5% of its customers to Burger Bills and 10% to Salty Sams each month.Salty Sams loses 10% of its customers to Burger Bills while 20% go to Hungry Heifer.What will the market shares be for the three businesses next month?

Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] -Using the data given in Table 14-4, find the equilibrium travel population for Frenzy (rounded to the nearest whole person).

Markov analysis assumes that while a member of one state may move to a different state over time, the overall makeup of the system will remain the same.

If we want to use Markov analysis to study market shares for competitive businesses

The vector of state probabilities for any period is equal to the vector of state probabilities for the preceding period multiplied by the matrix of transition probabilities.

Collectively exhaustive means that a system can be in only one state at any point in time.

There is a 30% chance that any current client of company A will switch to company B this year.There is a 20% chance that any client of company B will switch to company A this year.If these probabilities are stable over the years, and if company A has 1000 clients and company B has 1000 clients, in the long run (assuming the probabilities do not change), what will the market shares be?

Describe the concept of "collectively exhaustive" in the context of Markov analysis.

In Markov analysis, we also assume that the states are

The initial values for the state probabilities

There is a 60% chance that a customer without a smart phone will buy one this year.There is a 95% chance that a customer with a smart phone will continue with a smart phone going into the next year.If 30% of target market currently own smart phones, what is the long-run percentage of the target market that will own smart phones?

The vector of state probabilities for period n is (0.4, 0.6).The accompanying matrix of transition probabilities is: Calculate the vector of state probabilities for period n + 1.

One of the purposes of Markov analysis is to predict the future.

Table 14-6 The following data consists of a matrix of transition probabilities (P)of four majors in the College of Business, and the initial proportion of students in each major π(0).Assume that each state represents a major and the transition probabilities represent changes from one major to the next after taking the introductory class in each discipline. P = π(0)= (.4, .3, .2, .1) -Using the data in Table 14-6, determine Major 4's estimated popularity after students have taken the first two introductory courses.

In Markov analysis, initial-state probability values determine equilibrium conditions.

Table 14-3 The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees. A B C P = 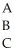π(0)= [1000, 1000, 1000) -Using the data given in Table 14-3, how many employees do we expect in location A one year from now?

Table 14-5 The following data consists of a matrix of transition probabilities (P)of three potential diseases, and the initial incidence of each disease π(0).Assume that each state represents a disease (Disease 1, Disease 2, Disease 3, respectively)and the transition probabilities represent changes from one checkup to the next. P = π(0)= (.3, .3, .4) -Using the data in Table 14-5, which disease will have the highest incidence when absorbing states are reached?

The four basic assumptions of Markov analysis are: There are a limited or finite number of possible states. The probability of changing states remains the same over time. A future state is predictable from previous state and transition matrix. The size and makeup of the system are constant during analysis.

Table 14-2 The following data consists of a matrix of transition probabilities (P)of three competing retailers, the initial market share π(0).Assume that each state represents a retailer (Retailer 1, Retailer 2, Retailer 3, respectively)and the transition probabilities represent changes from one month to the next. P = π(0)= (0.3, 0.6, 0.1) -Using the data given in Table 14-2, what is the equilibrium market share?