Exam 14: Markov Analysis

Table 14-5 The following data consists of a matrix of transition probabilities (P)of three potential diseases, and the initial incidence of each disease π(0).Assume that each state represents a disease (Disease 1, Disease 2, Disease 3, respectively)and the transition probabilities represent changes from one checkup to the next. P = π(0)= (.3, .3, .4) -Using the data in Table 14-5, determine Disease 3's estimated incidence in the next period.

A certain utility firm has noticed that a residential customer's bill for one month is dependent on the previous month's bill.The observations are summarized in the following transition matrix. 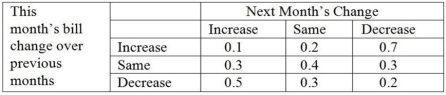The utility company would like to know the long-run probability that a customer's bill will increase, the probability the bill will stay the same, and the probability the bill will decrease.

Table 14-4 Cuthbert Wylinghauser is a scheduler of transportation for the state of Delirium.This state contains three cities: Chaos (C1), Frenzy (C2), and Tremor (C3).A transition matrix, indicating the probability that a resident in one city will travel to another, is given below.Cuthbert's job is to schedule the required number of seats, one to each person making the trip (transition), on a daily basis. C F T Transition matrix: π(0)= [100, 100, 100] -Using the data given in Table 14-4, what is the equilibrium travel population of Chaos (rounded to the nearest whole person)?