Question 1

What are some potential abuses or misuses of linear programming (beyond violation of basic assumptions)?

Accepted Answer

Answers will vary,but may include a discussion of the inability of modeling techniques to capture all of the relevant factors that may be as important as what can be quantified in an LP formulation.Factors such as aesthetics,ethics,civility,character,etc.,may be difficult to capture in an LP.Slavish adhesion to the output from a linear programming formulation robs a manager of the freedom to inject reality or personality into a model.The rush to use a tool without understanding fully the workings of it may render the output meaningless.

Question 2

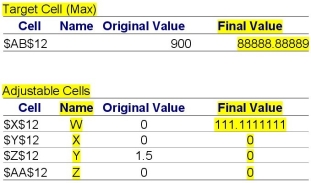
A very confused manager is reading a two-page report given to him by his student intern."She told me that she had my problem solved,gave me this,and then said she was off to her production management course," he whined."I gave her my best estimates of my on-hand inventories and requirements to produce,but what if my numbers are slightly off? I recognize the names of our four models W,X,Y,and Z,but that's about it.Can you figure out what I'm supposed to do and why?" You take the report from his hands and note that it is the answer report and the sensitivity report from Excel's solver routine.
Explain each of the highlighted cells in layman's terms and tell the manager what they mean in relation to his problem.
Microsoft Excel 10.0 Answer Report
Worksheet: Supplement D
Report Created: 1/26/2004 11:26:50 AM

Microsoft Excel 10.0 Sensitivity Report
Worksheet: Supplement D
Report Created: 1/26/2004 11:26:50 AM

Accepted Answer

Answer Report
Target Cell Max: The target cell should be maximized,so the manager must have provided the intern with profit information.
Final Value: The final value is the greatest amount possible for the situation.If we are working with profit figures,this is the best return possible given what we estimate is on hand and how it is to be produced.This may change if our inventory or recipes are slightly off.The highest profit identified is $88,888.89
Adjustable Cells: The adjustable cells show that we considered any positive quantity of models W-Z as possible outputs for the week.
Name: The names are those of the models we produce.
Final Value: These are the exact amounts of each of our four models to produce to earn the final value.In this case we would make 111.1 units of model W and none of the other four models.
Status: This shows what is limiting our ability to produce the models.A binding constraint directly limits our output although a nonbinding constraint means that factor does not limit us.In this case,the second and third constraints are nonbinding,so producing 111.1 units of model W leaves us with leftovers of whatever scarce resource they represent.The first constraint is binding,so we are using up every bit of that resource.
Slack: Slack shows us how much of each resource we have left.Our first constraint is binding,so we have none left over and therefore have 0 slack.Our second and third constraints are not binding,so we have plenty (3,888 and 25,000 units respectively)of these scarce resources left over.
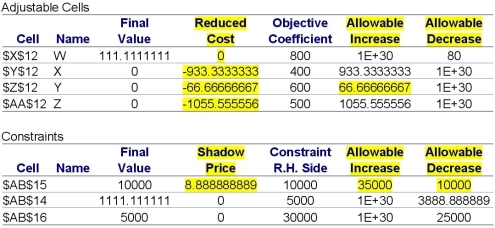
Sensitivity Report
Adjustable Cells
Reduced Cost: This is the change in the optimum objective per unit change in the upper or lower bounds of the variable.The objective function will increase by 0.-66,and so on,per unit increase.
Allowable Increase: These two (Allowable Increase and Allowable Decrease)provide a range for our current answer and the recipe we used to arrive at it.For model W,we have assumed that each unit gives us $800 profit.If our estimate was too high,and the return was up to $80 less per unit,we would still arrive at the same answer.If it were more than $80 too high,our answer would change.The same holds true for the models we are not making.If model Y made more than $666.66 profit per unit,then our final product mix would change.
Allowable Decrease: See analysis for Allowable Increase.
Constraints
Shadow Price: This is the marginal return for having one more unit of each resource.Here we have a shadow price of $8.88,so if we had one more unit of resource in the first constraint,we could make an additional $8.88.This gives us an idea of the maximum we would be willing to pay for more of that resource.
Allowable Increase: These work the same as the allowable increases and decreases for the adjustable cells except they focus on the shadow prices.They indicate how far the RHS of the constraint can change before the shadow price will change.
Allowable Decrease: See discussion immediately preceding.

Question 3

Consider a corner point to a linear programming problem,which lies at the intersection of the following two constraints:
6X1 + 15X2 ≤ 390
2X1 + X2 ≤ 50
Which of the following statements about the corner point is true?

Accepted Answer

A)  X1 ≤ 21 
B)  X1 ≥ 25 
C)  X1 ≤ 10 
D)  X1 ≥ 17 
A)  X1 ≤ 21 
B)  X1 ≥ 25 
C)  X1 ≤ 10 
D)  X1 ≥ 17 A

Question 4

The ________ problem is a one-period type of aggregate planning problem,the solution of which yields optimal output quantities of a group of products or services,subject to resource capacity and market demand conditions.

Accepted Answer

The answer of The ________ problem is a one-period type...

Question 5

A manager is interested in using linear programming to analyze production for the ensuing week.She knows that it will take exactly 1.5 hours to run a batch of product A and that this batch will consume two tons of sugar.This is an example of the linear programming assumption of

Accepted Answer

A)  linearity. 
B)  certainty. 
C)  continuous variables. 
D)  whole numbers. 
A)  linearity. 
B)  certainty. 
C)  continuous variables. 
D)  whole numbers.

Question 6

________ is an assumption that the decision variables must be either positive or zero.

Accepted Answer

The answer of ________ is an assumption that the decision...

Question 7

A snack food producer runs four different plants that supply product to four different regional distribution centers.The division operations manager is focused on one product,so he creates a table showing each plant's monthly capacity and each distribution center's monthly demand (both amounts in cases)for the product.The division manager supplements this table with the cost data to ship one case from each plant to each distribution center.Formulate an objective function and constraints that will solve this problem using linear programming.
 $$\begin{array} { | c | l | l | l | l | l | } 
\hline & \text { Center 1 } & \text { Center 2 } & \text { Center 3 } & \text { Center 4 } & \begin{array} { l } 
\text { Monthly } \
\text { Capacity }
\end{array} \
\hline \text { Plant A } & \$ 2 & \$ 7 & \$ 5 & \$ 4 & 8000 \
\hline \text { Plant B } & \$ 9 & \$ 4 & \$ 7 & \$ 6 & 12000 \
\hline \text { Plant C } & \$ 7 & \$ 6 & \$ 4 & \$ 3 & 7500 \
\hline \text { Plant D } & \$ 4 & \$ 8 & \$ 3 & \$ 5 & 5000 \
\hline \begin{array} { l } 
\text { Monthly } \
\text { Demand }
\end{array} & 9000 & 8500 & 8000 & 7000 & \
\hline
\end{array}$$

Accepted Answer

This is a cost minimization problem with

Question 8

A portfolio manager is trying to balance investments between bonds,stocks and cash.The return on stocks is 12 percent,9 percent on bonds,and 3 percent on cash.The total portfolio is $1 billion,and he or she must keep 10 percent in cash in accordance with company policy.The fund's prospectus promises that stocks cannot exceed 75 percent of the portfolio,and the ratio of stocks to bonds must equal two.Formulate this investment decision as a linear programming problem,defining fully your decision variables and then giving the objective function and constraints.

Accepted Answer

Let X₁ = the amount invested in bonds X₂=

Question 9

________ occurs in a linear programming problem when the number of nonzero variables in the optimal solution is fewer than the number of constraints.

Accepted Answer

The answer of ________ occurs in a linear programming problem...

Question 10

One assumption of linear programming is that a decision maker cannot use negative quantities of the decision variables.

Accepted Answer

A) True 
 B)False

Question 11

Provide three examples of operations management decision problems for which linear programming can be useful,and why.

Accepted Answer

Answers and justifications wil

Question 12

If merely rounding up or rounding down a result for a decision variable is not sufficient when they must be expressed in whole units,then a decision maker might instead use ________ to analyze the situation.

Accepted Answer

The answer of If merely rounding up or rounding down...

Question 13

Each coefficient or given constant is known by the decision maker with ________.

Accepted Answer

The answer of Each coefficient or given constant is known...

Question 14

What is the meaning of a slack or surplus variable?

Accepted Answer

The amount by which the left-h

Question 15

A(n)________ forms the optimal corner and limits the ability to improve the objective function.

Accepted Answer

The answer of A(n)________ forms the optimal corner and limits...

Question 16

Use the graphical technique to find the optimal solution for this objective function and associated constraints.
Maximize: Z=8A + 5B
Subject To:
Constraint 1 4A + 5B ≤80
Constraint 2 7A + 4B ≤ 120
A,B≥ 0
a.Graph the problem fully in the following space.Label the axes carefully,plot the constraints,shade the feasibility region,identify all candidate corner points,and indicate which one yields the optimal answer.

Accepted Answer

@#IMG-DLM& 
Intersection of Constraint 1 & 2
 \[\b

Question 17

A(n)________ is the marginal improvement in the objective function value caused by relaxing a constraint by one unit.

Accepted Answer

The answer of A(n)________ is the marginal improvement in the...

Question 18

A small oil company has a refining budget of $200,000 and would like to determine the optimal production plan for profitability.The following table lists the costs associated with its three products.
 $$\begin{array} { | c | c | c | c | } 
\hline \text { Product } & \begin{array} { c } 
\text { Refining } \
\text { Budget } \
\text { (\$ per unit of } \
\text { output) }
\end{array} & \begin{array} { c } 
\text { Marketing } \
\text { Budget } \
\text { (\$er unit of } \
\text { output) }
\end{array} & \begin{array} { c } 
\text { Material } \
\text { Availability } \
\text { (gallons of } \
\text { crude per unit } \
\text { of output) }
\end{array} \
\hline \text { Gasoline } & 0.40 & 0.10 & 10 \
\text { Heating Oil } & 0.10 & 0.05 & 5 \
\text { PlasticResin } & 0.60 & 0.07 & 20 \
\hline
\end{array}$$ 
Marketing has a budget of $50,000,and the company has 750,000 gallons of crude oil available.Each gallon of gasoline contributes 14 cents of profits,heating oil provides 10 cents,and plastic resin 30 cents per unit.The refining process results in a ratio of two units of heating oil for each unit of gasoline produced.This problem has been modeled as a linear programming problem and solved on the computer.The output follows:
Solution
 $\begin{array}{rrrr}
\text { Variable } & \begin{array}{r}
\text { Variable } \
\text { Vabel }
\end{array} & \begin{array}{r}
\text { Original } \
\text { Value }
\end{array} & \begin{array}{r}
\text { Coefficient } \
\text { Sensitivity }
\end{array} \
\text { Var1 } & 0.000 \mathrm{0} & 0.140 \mathrm{0}&0 \
\operatorname{Var}^{2} & 150000.000 \mathrm{0} & 0.100 \mathrm{0}&0 \
\operatorname{Var}^{3} & 0.000 \mathrm{0} & 0.300 \mathrm{0}&0
\end{array}$
$\begin{array}{rrrr}
\begin{array}{r}
\text { Constraint } \
\text { Label }
\end{array} & \begin{array}{r}
\text { Original } \
\text { RHV }
\end{array} & \begin{array}{r}
\text { Slack or } \
\text { Surplus }
\end{array} & \begin{array}{r}
\text { Shadow } \
\text { Price }
\end{array} \
\text { Const1 } & 20000 0 & 18500 0 & 0 \
\text { Const2 } & 5000 \mathrm{0} & 4250 \mathrm{0} & 0 \
\text { Const3 } & 75000 \mathrm{0} & 0 & 0.0200
\end{array}$

Objective Function
 Value:                                                                                        15000 
Sensitivity Analysis and Ranges
Objective Function Coefficients
 $$\begin{array} { r r r r } 
\text { Variable } & \text { Lower } & \text { Original } & \text { Upper } \
\text { Label } & \text { Limit } & \text { Coefficient } & \text { Limit } \\
\text { Var1 } & \text { No Limit } & 0.14 & 0.2 \
\text { Var2 } & 0.075 & 0.1 & \text { No Limit } \
\text { Var3 } & \text { No Limit } & 0.3 & 0.4
\end{array}$$ 
Right-Hand-Side Values
 $$\begin{array} { r r r r } 
\text { Constraint } & \text { Lower } & \text { Original } & \text { Upper } \
\text { Label } & \text { Limit } & \text { Value } & \text { Limit } \\
\text { Const1 } & 1500 0 & 20000 0 & \text { No Limit } \
\text { Const2 } & 750 0 & 5000 0 & \text { No Limit } \
\text { Const3 } & 0 & 75000 C & 5000000
\end{array}$$ 
a.Give a linear programming formulation for this problem.Make the variable definitions and constraints line up with the computer output.
b.What product mix maximizes the profit for the company using its limited resources?
c.How much gasoline is produced if profits are maximized?
d.Give a full explanation of the meaning of the three numbers listed following.
First Number: Slack or surplus of 42500 for constraint 2.
Second Number: Shadow price of 0 for constraint 1.
Third Number: An upper limit of "no limit" for the right-hand-side value constraint 1.

Accepted Answer

a.Let X₁= gallons of gasoline refined X₂=

Question 19

For an = constraint,only points ________ are feasible solutions.

Accepted Answer

The answer of For an = constraint,only points ________ are...

Question 20

Briefly describe the meaning of a shadow price.Provide an example of how a manager could use information about shadow prices to improve operations?

Accepted Answer

The shadow price is the margin

What are some potential abuses or misuses of linear programming (beyond violation of basic assumptions)?

Consider a corner point to a linear programming problem,which lies at the intersection of the following two constraints: 6X₁ + 15X₂ ≤ 390 2X₁+ X₂ ≤ 50 Which of the following statements about the corner point is true?

The ________ problem is a one-period type of aggregate planning problem,the solution of which yields optimal output quantities of a group of products or services,subject to resource capacity and market demand conditions.

A manager is interested in using linear programming to analyze production for the ensuing week.She knows that it will take exactly 1.5 hours to run a batch of product A and that this batch will consume two tons of sugar.This is an example of the linear programming assumption of

________ is an assumption that the decision variables must be either positive or zero.

________ occurs in a linear programming problem when the number of nonzero variables in the optimal solution is fewer than the number of constraints.

One assumption of linear programming is that a decision maker cannot use negative quantities of the decision variables.

Provide three examples of operations management decision problems for which linear programming can be useful,and why.

If merely rounding up or rounding down a result for a decision variable is not sufficient when they must be expressed in whole units,then a decision maker might instead use ________ to analyze the situation.

Each coefficient or given constant is known by the decision maker with ________.

What is the meaning of a slack or surplus variable?

A(n)________ forms the optimal corner and limits the ability to improve the objective function.

A(n)________ is the marginal improvement in the objective function value caused by relaxing a constraint by one unit.

For an = constraint,only points ________ are feasible solutions.

Briefly describe the meaning of a shadow price.Provide an example of how a manager could use information about shadow prices to improve operations?

Creating Customer Value through Operations

Supply Chain Management

Process Configuration

Capacity

Inventory Management

Quality and Process Improvement

Lean Systems

Managing Projects

Location and Layout

Managing Demand and Forecasting

Operations Planning and Scheduling

Resource Planning

Decision Making

Financial Analysis

Work Measurement

Learning Curve Analysis

Computer-Integrated Manufacturing

Acceptance Sampling Plans

Simulation

Special Inventory Models

Waiting Lines

Filters

Exam 21: Linear Programming

What are some potential abuses or misuses of linear programming (beyond violation of basic assumptions)?

Consider a corner point to a linear programming problem,which lies at the intersection of the following two constraints: 6X1 + 15X2 ≤ 390 2X1 + X2 ≤ 50 Which of the following statements about the corner point is true?

The ________ problem is a one-period type of aggregate planning problem,the solution of which yields optimal output quantities of a group of products or services,subject to resource capacity and market demand conditions.

A manager is interested in using linear programming to analyze production for the ensuing week.She knows that it will take exactly 1.5 hours to run a batch of product A and that this batch will consume two tons of sugar.This is an example of the linear programming assumption of

________ is an assumption that the decision variables must be either positive or zero.

________ occurs in a linear programming problem when the number of nonzero variables in the optimal solution is fewer than the number of constraints.

One assumption of linear programming is that a decision maker cannot use negative quantities of the decision variables.

Provide three examples of operations management decision problems for which linear programming can be useful,and why.

If merely rounding up or rounding down a result for a decision variable is not sufficient when they must be expressed in whole units,then a decision maker might instead use ________ to analyze the situation.

Each coefficient or given constant is known by the decision maker with ________.

What is the meaning of a slack or surplus variable?

A(n)________ forms the optimal corner and limits the ability to improve the objective function.

A(n)________ is the marginal improvement in the objective function value caused by relaxing a constraint by one unit.

For an = constraint,only points ________ are feasible solutions.

Briefly describe the meaning of a shadow price.Provide an example of how a manager could use information about shadow prices to improve operations?

Creating Customer Value through Operations

Supply Chain Management

Process Configuration

Capacity

Inventory Management

Quality and Process Improvement

Lean Systems

Managing Projects

Location and Layout

Managing Demand and Forecasting

Operations Planning and Scheduling

Resource Planning

Decision Making

Financial Analysis

Work Measurement

Learning Curve Analysis

Computer-Integrated Manufacturing

Acceptance Sampling Plans

Simulation

Special Inventory Models

Waiting Lines

Filters

Consider a corner point to a linear programming problem,which lies at the intersection of the following two constraints: 6X₁ + 15X₂ ≤ 390 2X₁+ X₂ ≤ 50 Which of the following statements about the corner point is true?