Exam 10: Topics In Analytic Geometry
Exam 1: Functions and Their Graphs513 Questions
Exam 2: Polynomial and Rational Functions456 Questions
Exam 3: Exponential and Logarithmic Functions266 Questions
Exam 4: Trigonometry384 Questions
Exam 5: Analytic Trigonometry265 Questions
Exam 6: Additional Topics In Trigonometery304 Questions
Exam 7: Systems Of Equations and Inequalities305 Questions
Exam 8: Matrices and Determinants283 Questions
Exam 9: Sequences Series and Probability405 Questions
Exam 10: Topics In Analytic Geometry556 Questions
Exam 11: Analytic Geometry In Three Dimensions256 Questions
Exam 12: Limits and An Introduction To Calculus259 Questions
Select questions type
A point in polar coordinates is given.Convert the point to rectangular coordinates.Round your answers to one decimal places.
(Multiple Choice)
4.9/5  (42)
(42)
By using a graphing utility select the correct graph of the polar equation.Identify the graph.
(Multiple Choice)
5.0/5  (34)
(34)
Eliminate the parameter and write the corresponding rectangular equation whose graph represents the curve.
(Multiple Choice)
4.9/5  (38)
(38)
Select the curve represented by the parametric equations. x=5\theta y=6\theta
(Multiple Choice)
4.8/5  (39)
(39)
Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. Horizontal axis and passes through the point
(Multiple Choice)
4.9/5  (34)
(34)
The receiver in a parabolic satellite dish is 4.5 feet from the vertex and is located at the focus (see figure).Write an equation for a cross section of the reflector.(Assume that the dish is directed upward and the vertex is at the origin.) 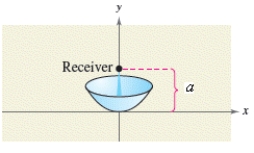
(Multiple Choice)
4.8/5  (34)
(34)
Identify the equation as a circle, a parabola, an ellipse, or a hyperbola.
(Multiple Choice)
4.9/5  (37)
(37)
Select the correct graph of the polar equation.Describe your viewing window.
(Multiple Choice)
4.7/5  (40)
(40)
Find the standard form of the equation of the parabola with the given characteristic and vertex at the origin. focus: (0, -4)
(Multiple Choice)
4.9/5  (31)
(31)
Select the graph of the polar equation using symmetry, zeros, maximum r-values, and any other additional points.
(Multiple Choice)
4.9/5  (46)
(46)
Select the correct graph of the polar equation.Find an interval for for which the graph is traced only once.
(Multiple Choice)
4.8/5  (38)
(38)
Find the standard form of the equation of the parabola with the given characteristic(s) and vertex at the origin.
Passes through the point ; vertical axis
(Multiple Choice)
4.7/5  (48)
(48)
Find the rectangular coordinates of the point given in polar coordinates.Round your results to two decimal places.
(Multiple Choice)
4.7/5  (46)
(46)
A projectile is launched at a height of h feet above the ground at an angle of with the horizontal.The initial velocity is feet per second, and the path of the projectile is modeled by the parametric equations . Select the correct graph of the path of a projectile launched from ground level at the value of and .
feet per second
(Multiple Choice)
4.8/5  (28)
(28)
Using following result find a set of parametric equation of the line.
Line: passes through (0,0) and
(Multiple Choice)
4.9/5  (31)
(31)
Showing 461 - 480 of 556
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)