Exam 2: Nonlinear Functions and Models
Exam 1: Functions and Applications159 Questions
Exam 2: Nonlinear Functions and Models92 Questions
Exam 3: The Mathematics of Finance137 Questions
Exam 4: Systems of Linear Equations and Matrices111 Questions
Exam 5: Matrix Algebra and Applications174 Questions
Exam 6: Linear Programming161 Questions
Exam 7: Sets and Counting154 Questions
Exam 8: Probability257 Questions
Exam 9: Random Variables and Statistics178 Questions
Exam 10: Introduction to the Derivative139 Questions
Exam 11: Techniques of Differentiation104 Questions
Exam 12: Applications of the Derivative88 Questions
Exam 13: The Integral66 Questions
Exam 14: Further Integration Techniques and Applications of the Integral118 Questions
Exam 15: Functions of Several Variables137 Questions
Exam 16: Trigonometric Models67 Questions
Select questions type
Plutonium-239 is used as a fuel for some nuclear reactors and also as the fissionable material in atomic bombs. It has a half-life of 24,400 years. How long will it take 12 grams of plutonium-239 to decay to 2 grams ?
Round your answer to the nearest hundreds.
(Multiple Choice)
4.8/5  (34)
(34)
Convert the exponential function to the form indicated. Round all coefficients to four significant digits.
;
(Multiple Choice)
4.8/5  (33)
(33)
Soon after taking an aspirin, a patient has absorbed 350 mg of the drug. If the amount of aspirin in the bloodstream decays exponentially, with half being removed every 2 hours, find the time it will take for the amount of aspirin in the bloodstream to decrease to 260 mg.
Select the answer rounded to three decimal places.
(Multiple Choice)
4.7/5  (35)
(35)
The U.S. population was 170 million in 1950 and 240 million in 1990. Assuming exponential population growth, what will the population be in the year 2020 Round your answer to the nearest million.
Select the correct answer.
(Multiple Choice)
4.8/5  (37)
(37)
Encouraged by the popularity of your Dungeons and Dragons website, www.mudbeast.net, you have decided to charge users who log on to the site. When you charged a $1.50 access fee, your web counter showed a demand of 270 "hits" per month. After you lowered the price to $0.50, activity increased to 350 "hits" per month. Obtain the monthly revenue R as a function of the access fee x.
(Multiple Choice)
4.8/5  (32)
(32)
Which of the following five functions will be smallest for large values of x
Select the correct answer.
(Multiple Choice)
4.7/5  (30)
(30)
The table lists interest rates on long-term investments (based on 10-year government bonds) in several countries in 2004-2005. Assuming that you invest $12,000 in Japan, how long (to the nearest year) must you wait before your investment is worth $18,000 if the interest is compounded annually Country U.S. Japan Canada Yield 5.3\% 1.5\% 5.2\%
__________ year(s)
(Short Answer)
4.9/5  (36)
(36)
The given table corresponds to the function . -3 -2 -1 0 1 2 3 ( ) 0.084 0.067 0.067 1 0.033 0.027 0.021
(True/False)
4.8/5  (37)
(37)
The amount of carbon-14 remaining in a sample that weighs B is given by
where t is time in years. If tests on a fossilized skull reveal that 99.92% of the carbon-14 has decayed, how old is the skull
Select the correct answer rounded to the nearest integer.
(Multiple Choice)
4.8/5  (39)
(39)
Model the data using an exponential function . 0 1 2 f(x) 300 75 18.75
(Essay)
4.8/5  (46)
(46)
Find an equation for an exponential function that passes through the pair of points and .
(Multiple Choice)
4.9/5  (30)
(30)
Find the logistic function f with the given properties. , f has limiting value 20, and for small values of x, f is approximately exponential and grows by 50% with every increase of 1 in x.
(Multiple Choice)
4.8/5  (41)
(41)
The chart shows the number of research articles in the prominent journal Physics Review that were written by researchers in Europe during 1983 - 2003 ( represents 1983). 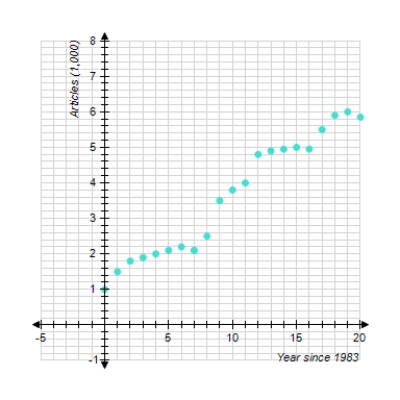 Which of the following logistic functions best models the data (t is the number of years since 1983.) Try to determine the correct model without actually computing data points.
Which of the following logistic functions best models the data (t is the number of years since 1983.) Try to determine the correct model without actually computing data points.
(Multiple Choice)
4.8/5  (38)
(38)
The graph shows the actual percentage of U.S. households with a computer as a function of household income (the data points) and a logistic model of these data (the curve). The logistic model is
where x is the household income in thousands of dollars. According to the model, what percentage of extremely wealthy households had computers
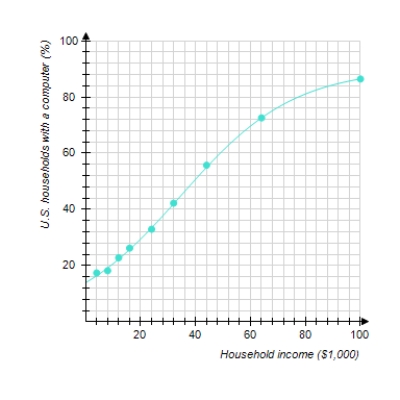 P = __________%
P = __________%
(Short Answer)
4.8/5  (24)
(24)
Use technology to find a logistic regression curve approximating the given data. (Round b to three significant digits and A and N to two significant digits.) x 0 20 40 60 80 100 y 2.2 3.8 5.0 6.1 6.8 6.9
(Multiple Choice)
4.8/5  (36)
(36)
Model the data using an exponential function . 0 1 2 ( ) 350 175 87.5 Select the correct answer.
(Multiple Choice)
4.9/5  (33)
(33)
The following graph shows the actual percentage of U.S. households with a computer as a function of household income (the data points) and a logistic model of these data (the curve). The logistic model is
Where x is the household income in thousands of dollars. For low incomes, the logistic model is approximately exponential. Which exponential model best approximates P(x) for small x Round the coefficients to the nearest hundredth.
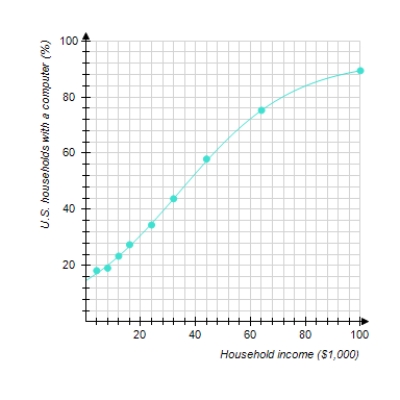
(Multiple Choice)
4.9/5  (32)
(32)
Use logarithms to solve the equation. Round your answer to four decimal places.
(Multiple Choice)
4.7/5  (30)
(30)
Showing 21 - 40 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)