Exam 12: Comparing Multiple Proportions, Tests of Independence and Goodness of Fit
Exam 1: Data and Statistics84 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays67 Questions
Exam 3: Descriptive Statistics: Numerical Measures118 Questions
Exam 4: Introduction to Probability94 Questions
Exam 5: Discrete Probability Distributions84 Questions
Exam 6: Continuous Probability Distributions121 Questions
Exam 7: Sampling and Sampling Distributions116 Questions
Exam 8: Interval Estimation90 Questions
Exam 9: Hypothesis Tests95 Questions
Exam 10: Inference About Means and Proportions With Two Populations63 Questions
Exam 11: Inferences About Population Variances66 Questions
Exam 12: Comparing Multiple Proportions, Tests of Independence and Goodness of Fit59 Questions
Exam 13: Experimental Design and Analysis of Variance76 Questions
Exam 14: Simple Linear Regression132 Questions
Exam 15: Multiple Regression103 Questions
Exam 16: Regression Analysis: Model Building41 Questions
Exam 17: Time Series Analysis and Forecasting51 Questions
Exam 18: Nonparametric Methods58 Questions
Exam 19: Decision Analysis48 Questions
Exam 20: Index Numbers39 Questions
Exam 21: Statistical Methods for Quality Control60 Questions
Exam 22: Sample Survey48 Questions
Select questions type
In 2002, 40% of the students at a major university were Business majors, 35% were Engineering majors, and the rest of the students were majoring in other fields. In a sample of 600 students from the same university taken in 2003, 200 were Business majors, 220 were Engineering majors, and the remaining students in the sample were majoring in other fields. Using α = .01, test to see if there has been a significant change in the proportions between 2002 and 2003.
(Essay)
4.9/5  (31)
(31)
When individuals in a sample of 150 were asked whether or not they supported capital punishment, the following information was obtained. 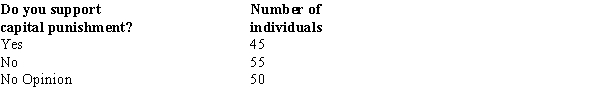 We are interested in determining whether or not the opinions of the individuals (as to Yes, No, and No Opinion) are uniformly distributed. The calculated value for the test statistic equals
We are interested in determining whether or not the opinions of the individuals (as to Yes, No, and No Opinion) are uniformly distributed. The calculated value for the test statistic equals
(Multiple Choice)
4.8/5  (27)
(27)
The personnel department of a large corporation reported sixty resignations during the last year. The following table groups these resignations according to the season during which they occurred: 
Test to see if the proportion of resignations is uniform over the four seasons.
Let α = .05.
Test to see if the proportion of resignations is uniform over the four seasons.
Let α = .05.
(Essay)
4.9/5  (38)
(38)
When individuals in a sample of 150 were asked whether or not they supported capital punishment, the following information was obtained. 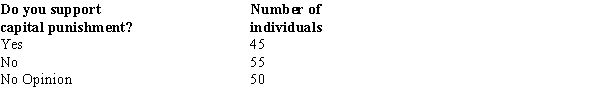 We are interested in determining whether or not the opinions of the individuals (as to Yes, No, and No Opinion) are uniformly distributed. The number of degrees of freedom associated with this problem is
We are interested in determining whether or not the opinions of the individuals (as to Yes, No, and No Opinion) are uniformly distributed. The number of degrees of freedom associated with this problem is
(Multiple Choice)
4.7/5  (31)
(31)
Shown below is a 2 x 3 table with observed values from a sample of 500. At α = .05 using the critical value approach, test for independence of the row and column factors. 
(Essay)
4.7/5  (38)
(38)
In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students from the university was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College. The hypothesis is to be tested at the 5% level of significance. The critical value from the table equals
(Multiple Choice)
4.8/5  (37)
(37)
When individuals in a sample of 150 were asked whether or not they supported capital punishment, the following information was obtained. 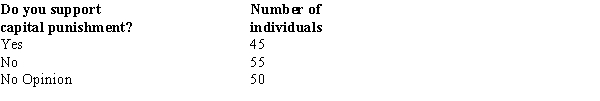 We are interested in determining whether or not the opinions of the individuals (as to Yes, No, and No Opinion) are uniformly distributed. The p-value is
We are interested in determining whether or not the opinions of the individuals (as to Yes, No, and No Opinion) are uniformly distributed. The p-value is
(Multiple Choice)
4.7/5  (37)
(37)
An insurance company has gathered the following information regarding the number of accidents reported per day over a period of 100 days. 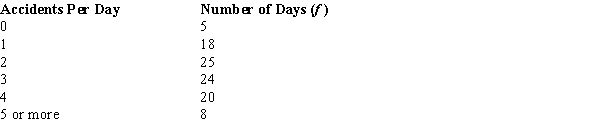
Using the critical value approach, test to see if the above data have a Poisson distribution. Let α = .05.
Using the critical value approach, test to see if the above data have a Poisson distribution. Let α = .05.
(Essay)
4.8/5  (41)
(41)
The following table shows the number of individuals in a sample of 450 who indicated they support the new tax proposal.  We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed. The expected frequency for each group is
We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed. The expected frequency for each group is
(Multiple Choice)
4.8/5  (28)
(28)
You want to test whether or not the following sample of 30 observations follows a normal distribution. The mean of the sample equals 11.83 and the standard deviation equals 4.53. 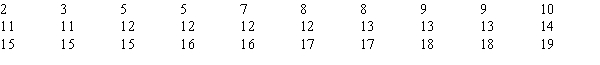 The p-value is
The p-value is
(Multiple Choice)
4.8/5  (37)
(37)
Shown below is 3 x 2 table with observed values from a sample of 1500. At the 5% level of significance, test for independence of the row and column factors. 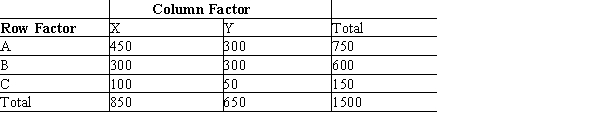
(Essay)
4.8/5  (33)
(33)
You want to test whether or not the following sample of 30 observations follows a normal distribution. The mean of the sample equals 11.83 and the standard deviation equals 4.53. 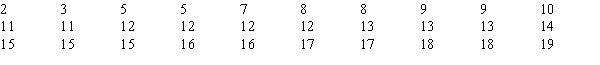 The number of intervals or categories used to test the hypothesis for this problem is
The number of intervals or categories used to test the hypothesis for this problem is
(Multiple Choice)
4.9/5  (32)
(32)
Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 400 students taken from this year's student body showed the following number of students in each classification.  We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year. The expected number of freshmen is
We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year. The expected number of freshmen is
(Multiple Choice)
4.7/5  (30)
(30)
The following data show the scores of a sample of 40 students who have taken statistics. 
Use α = .10 and conduct a goodness of fit test to determine if the sample comes from a population that has a normal distribution. Use the critical value approach.
Use α = .10 and conduct a goodness of fit test to determine if the sample comes from a population that has a normal distribution. Use the critical value approach.
(Essay)
4.7/5  (33)
(33)
Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 400 students taken from this year's student body showed the following number of students in each classification.  We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year. The calculated value for the test statistic equals
We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year. The calculated value for the test statistic equals
(Multiple Choice)
4.7/5  (40)
(40)
The table below gives beverage preferences for random samples of teens and adults. 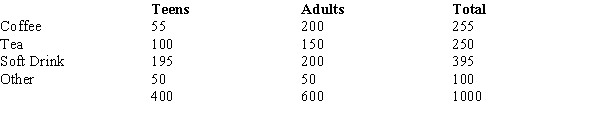 We are asked to test for independence between age (i.e., adult and teen) and drink preferences. The expected number of adults who prefer coffee is
We are asked to test for independence between age (i.e., adult and teen) and drink preferences. The expected number of adults who prefer coffee is
(Multiple Choice)
5.0/5  (30)
(30)
From a poll of 800 television viewers, the following data have been accumulated as to their levels of education and their preference of television stations. 
Test at α = .05 to determine if the selection of a TV station is dependent upon the level of education. Use the p-value approach.
Test at α = .05 to determine if the selection of a TV station is dependent upon the level of education. Use the p-value approach.
(Essay)
4.8/5  (36)
(36)
The table below gives beverage preferences for random samples of teens and adults. 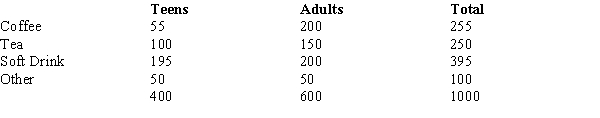 We are asked to test for independence between age (i.e., adult and teen) and drink preferences. With a .05 level of significance, the critical value for the test is
We are asked to test for independence between age (i.e., adult and teen) and drink preferences. With a .05 level of significance, the critical value for the test is
(Multiple Choice)
5.0/5  (31)
(31)
Showing 41 - 59 of 59
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)