Exam 15: Analysis of Variance
Exam 1: The Role of Statistics and the Data Analysis Process17 Questions
Exam 2: Collecting Data Sensibly39 Questions
Exam 3: Graphical Methods for Describing Data25 Questions
Exam 4: Numerical Methods for Describing Data26 Questions
Exam 5: Summarizing Bivariate Data37 Questions
Exam 6: Probability34 Questions
Exam 7: Random Variables and Probability Distributions45 Questions
Exam 8: Sampling Variability and Sampling Distributions27 Questions
Exam 9: Estimation Using a Single Sample46 Questions
Exam 10: Hypothesis Testing Using a Single Sample37 Questions
Exam 11: Comparing Two Populations or Treatments42 Questions
Exam 12: The Analysis of Categorical Data and Goodness-Of-Fit Tests21 Questions
Exam 13: Simple Linear Regression and Correlation: Inferential Methods56 Questions
Exam 14: Multiple Regression Analysis38 Questions
Exam 15: Analysis of Variance40 Questions
Exam 16: Nonparametric Distribution-Free Statistical Methods15 Questions
Select questions type
If the line segments in an interaction plot are parallel, then the plot indicates that the two factors interact with each other.
Free
(True/False)
4.8/5  (36)
(36)
Correct Answer:
False
When using the Tukey-Kramer multiple comparison procedure, if the confidence interval for μ1 − μ2 contains 0 then μ1 and μ2 are declared to be significantly different.
Free
(True/False)
4.8/5  (33)
(33)
Correct Answer:
False
The test statistic for testing the equality of population means in a single-factor ANOVA is 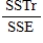 .
.
Free
(True/False)
4.8/5  (29)
(29)
Correct Answer:
False
When using the 95% Tukey-Kramer procedure, in the long run only about 5% of time would at least one of the intervals not include the value that is being estimated.
(True/False)
4.8/5  (27)
(27)
Nutritionists study the impact of four different diets on women's vulnerability to vitamin B6 deficiency. The researchers randomly assigned adult women to one of four groups. Each group followed a specific diet. Let µ1, µ2, µ3, and µ4 represent the mean daily intake of vitamin B6 (in mg) for diets 1, 2, 3, and 4, respectively. The sample data are given in the table below. Use the 95% Tukey-Kramer procedure to identify the correct statement describing the differences among the diets. 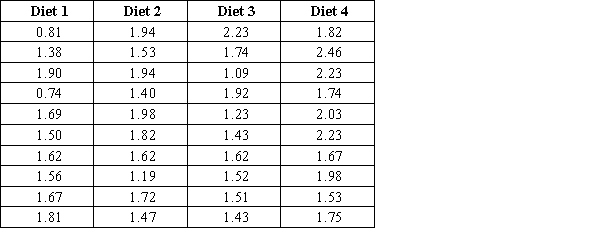
(Multiple Choice)
4.8/5  (32)
(32)
In a two-factor ANOVA the main effects of factors A and B should be tested before testing for the presence of the interaction.
(True/False)
4.8/5  (35)
(35)
Two factors A and B are said to interact when the change in the true average response when the level of one factor changes depends on the level of the other factor.
(True/False)
4.8/5  (40)
(40)
A dairy scientist is studying three different formulas that could be used in producing low fat cheese. The experimental process involves mixing the basic cheese ingredients in 4 different vats (blocks) and then splitting the mixture from each vat into three different batches. Additives are added to each of the batches according to each of the three formulas resulting in a round of low fat cheese. The data below represents the fat content (in grams per ounce) of the resulting rounds of cheese for this randomized block design. 
a) Construct the ANOVA table for this experiment.
b) Test the equality of the mean fat content for the three different low fat cheese formulas at the .05 level.
c) Using the 95% Tukey-Kramer procedure determine which of the treatment means are significantly different.
a) Construct the ANOVA table for this experiment.
b) Test the equality of the mean fat content for the three different low fat cheese formulas at the .05 level.
c) Using the 95% Tukey-Kramer procedure determine which of the treatment means are significantly different.
(Essay)
4.9/5  (36)
(36)
A comparison of the treatments based on independently selected experimental units that are randomly assigned to treatments is referred to as a completely randomized design.
(True/False)
4.9/5  (40)
(40)
The Tukey-Kramer procedure controls the simultaneous confidence level.
(True/False)
4.9/5  (36)
(36)
Briefly explain how to check the assumption of normality in a single-factor ANOVA.
(Essay)
4.8/5  (34)
(34)
The following partial ANOVA table was based on a randomized block experiment with 5 treatments and 5 blocks. 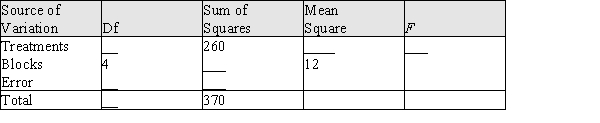 a) Fill in the missing entries in the ANOVA table. b) Test the equality of the treatment means using a .05 significance level. c) If the five treatment means are
a) Fill in the missing entries in the ANOVA table. b) Test the equality of the treatment means using a .05 significance level. c) If the five treatment means are 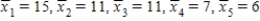 use the 95% Tukey-Kramer procedure to determine which means differ.
use the 95% Tukey-Kramer procedure to determine which means differ.
(Essay)
4.9/5  (31)
(31)
A veterinarian is studying three different medications that could be used in the prevention of heartworm in young puppies. She has acquired for study four different litters of cocker spaniels, and 3 puppies were randomly selected from each litter. The three selected puppies from a litter were then randomly assigned to one of the four treatments. The data below represents the number of months after a single treatment before the initial onset of heartworm in the puppies for this randomized block design.  a) Construct the ANOVA table for this experiment. b) Test the equality of the mean time to onset of heartworm for the three different medications at the .05 level. c) Using the 95% Tukey-Kramer procedure determine which of the treatment means are significantly different.
a) Construct the ANOVA table for this experiment. b) Test the equality of the mean time to onset of heartworm for the three different medications at the .05 level. c) Using the 95% Tukey-Kramer procedure determine which of the treatment means are significantly different.
(Essay)
4.9/5  (38)
(38)
What are the assumptions of the randomized block ANOVA F test for testing the equality of treatment means?
(Essay)
4.9/5  (35)
(35)
An experiment was designed to investigate the effectiveness of 5 different methods that are used for decontaminating topsoil. Each of the 5 methods is applied to a plot of contaminated soil at 3 different Superfund sites (blocks) and the reduction in heavy metals in the topsoil is recorded. The experiment yields the following summary information. SSTo = 1,209.3 SSTr = 635.8 SSBl = 297.6
a) Construct the ANOVA table for this experiment.
b) Test for the null hypothesis that there is no difference in the mean reduction of heavy metals for the 5 different methods using a .05 significance level.
(Essay)
4.8/5  (30)
(30)
A construction engineer has designed an experiment to investigate 3 different types of pressure treatment that can be applied to raw lumber. The experiment was conducted as a completely randomized design in which 30 pieces of raw lumber were selected with 10 assigned at random to each of the three pressure treatments. The response variable was water repellency. The sample means and the sum of squared error are given below.  SSE = 168.2
a) Construct the ANOVA table for this experiment.
b) Test the equality of the means of the three different treatments using a .05 significance level.
c) Using the 95% Tukey-Kramer procedure determine which pairs of means are significantly different.
SSE = 168.2
a) Construct the ANOVA table for this experiment.
b) Test the equality of the means of the three different treatments using a .05 significance level.
c) Using the 95% Tukey-Kramer procedure determine which pairs of means are significantly different.
(Essay)
4.9/5  (43)
(43)
In a randomized block design having 10 treatments and 5 blocks with each treatment occurring once in each block, there are 36 degrees of freedom for the error source of variation.
(True/False)
4.9/5  (40)
(40)
In a two-factor ANOVA with k levels of factor A and l levels of factor B, the number of treatment combinations is k + l.
(True/False)
4.8/5  (35)
(35)
A study investigating the effectiveness of 4 different brands of mosquito repellent was performed as a completely randomized design. The results of the experiment are given in the table below for the response variable y = the length of effectiveness of a single application of mosquito repellent.  SSE = 115.2
a) Construct ANOVA table for this experiment.
b) Test the equality of the means of the four different brands of mosquito repellent at the .05 level.
c) Using the 95% Tukey-Kramer procedure determine which pairs of means are significantly different.
SSE = 115.2
a) Construct ANOVA table for this experiment.
b) Test the equality of the means of the four different brands of mosquito repellent at the .05 level.
c) Using the 95% Tukey-Kramer procedure determine which pairs of means are significantly different.
(Essay)
4.8/5  (33)
(33)
Showing 1 - 20 of 40
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)